Middle School

Happy Accidents
When I was growing up in (rural-ish) central New York, we had one TV. We received 5 local stations through the antenna on the roof (abc, nbc, occasionally cbs if the wind was blowing just right, then Fox came along, and a pbs station). This was a time when TV programming on the major networks actually ended at about 1:00 a.m. with a video of the American flag waving in the wind and the national anthem playing. When that was over, there was nothing on TV but static. This is something my kids can’t imagine. Not that they watch regular TV that often anyway (YouTube, Vimeo, etc.), but every time they turn it on, there are at least 100 shows to choose from on 4 TVs.
This wasn’t the case for my siblings and me. Usually, the first person in the living room got dibs on what show was on or there had to be a “discussion” to figure out what everyone would watch. Sometimes this ended in the TV being turned off by Mom or Dad with a “suggestion” that we go outside and get some fresh air. Other times, we would decide to figure it out on our own and end up on the local PBS station watching a man with a huge perm (this was the 1980s) paint beautiful scenes in about 25 minutes.

We (my 5 siblings and I) were all in awe while we watched Bob Ross paint wonderful paintings while talking to us (the viewers) about everything from his pet squirrels to painting techniques. And at the end of every episode I felt like I could paint just like Bob Ross! I never tried, but I felt like I could!
Recently, my kids have discovered the talent and wonder of Bob Ross through YouTube and Netflix. They love his words of wisdom:
- “Just go out and talk to a tree. Make friends with it.”
- “There’s nothing wrong with having a tree as a friend.”
- “How do you make a round circle with a square knife? That’s your challenge for the day.”
- “Any time ya learn, ya gain.”
- “You can do anything you want to do. This is your world.”
And I love that they love these words of wisdom. You can find more here.
For Christmas this year, my son and I received Bob Ross T-shirts. Connor’s has just an image, while mine has a quote as well:

Bob Ross was referring to painting when he said these words; “In painting there are no mistakes, just happy accidents.” In other words, when you paint your mountain the wrong shape, treat it as a happy accident. It can still be a mountain, there may just end up being a happy tree or a happy cloud that takes care of your happy accident.
I think it works for math class, too. Recently, I modeled a Desmos lesson for a 7th grade teacher. The students had been working with expressions and equations but were struggling with the abstract ideas associated with expressions and equations. The teacher and I planned for me to model Desmos using Central Park to see how students reacted to the platform (this was their first time using Desmos) and how I managed the class using the teacher dashboard.
During the lesson, there was a lot of productive struggle. Students were working in pairs and making mistakes happy accidents. They were happy accidents! Because students kept going back for more. At times there was some frustration involved and I stepped in to ask questions like:
- What are you trying to figure out?
- Where did the numbers you used in your expression come from?
- What do each of the numbers you used represent?
- Before you click the “try it” button, how confident are you that the cars will all park?
The last question was incredibly informative. Many students who answered this question were not confident at all that their cars would all park, but as they moved through the lesson, their confidence grew.
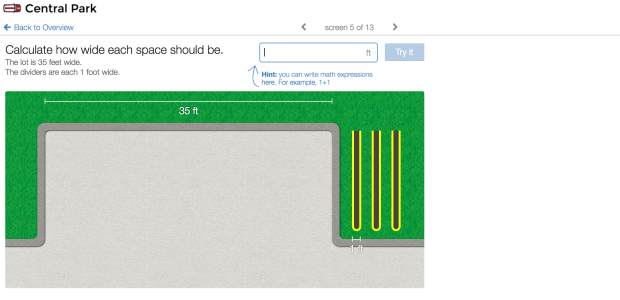
One of the best take-aways the teacher mentioned during our post-conference was when she mentioned a certain boy and girl who she paired together so the (high performing) girl could help the (low performing) boy. The exact opposite happened. The girl was trying to crunch numbers on screen 5 with little success. The boy just needed a nudge to think about the image and to go back to some previous screens to settle some ideas in his mind before moving ahead with his idea that the answer is 8. Then, he got to expain how he knew it was 8 with the picture, conceptually, to his partner. The teacher’s mistake happy accident was in believing her students would always perform a certain way. When students are engaged in tasks that are meaningful, they tend to perform differently than when they’re given a worksheet with 30 meaningless problems on it (the norm for this class before Desmos). Ah-has all around and the “low student” shows that he knows more than the teacher thinks.
The icing on the cake? Several students walking out of the classroom could be heard saying, “That was cool.” or “That was fun.”
Let’s treat math mistakes as happy accidents, something to learn from and problem solve our way through. When students (all humans) make a mistake, synapses fire. The brain grows (More on this from Jo Boaler here). What we do as teachers from this point, determines how much more the brain will grow. If we treat student mistakes as happy accidents, perhaps their brains will grow a bit more than if we continue to treat mistakes in the traditional manner.
Let’s hear it for Bob Ross. He probably never thought his words of wisdom about painting would be translated to the math classroom.
Now, go make friends with a math problem.
Connecting Percents and Fractions
Not understanding mathematics can be extremely frustrating for students. As a teacher, figuring out how to help students understand mathematics can be just as frustrating. My primary go-to resource for these situations is Teaching Student-Centered Mathematics, by John Van de Walle et. al. because it’s all about focusing on big ideas and helping students make sense of the math they’re learning in a conceptual way.
Recently, I was asked to model a lesson for a 6th grade class who was having difficulty working with percents. So, I turned to my go-to resource, and during planning, I realized that I didn’t know anything about these students other than that they were struggling with percents. So, I couldn’t assume anything. I ended up creating three separate lessons and combined them into 1.
First, I handed groups of students a set of Percent Cards and Circle Graph Cards. Their task was to match the percent with the corresponding circle graph. As students were working on this, I heard groups reasoning about how they were matching the cards. Many started with benchmarks of 25%, 50%, and 75%, while others started with the smallest (10%) and matching it to the graph with the smallest wedge. As groups finished, they were asked to find pairs, using the matches they made, that totaled 100%. Once finished, a discussion about their process for completing these tasks revealed a solid understanding of percent as representing a part of a whole.
Now to shake their world up a bit. I asked them to leave their cards because they would be using them again shortly. I introduced these Percent circles and asked them what they were. A brief discussion revealed some misconceptions. Some students said they were fractions, others said they were wholes because nothing was shaded. I altered my planned line of questioning to questions that eventually led to a common understanding of what fractions were and how the pictures of the fraction (percent) circles really showed wholes and parts (fractions).
Their next task was to match their cards with the equivalent fraction circle. This was incredibly eye-opening. Groups began to notice that some percent card matches could fit with multiple fraction circles (50% could be matched with the halves, quarters, eighths, and tenths). Thirds and eighths were the last to be matched. But their reasoning didn’t disappoint. One group noticed that the percents ending in .5 all belonged with the eighths because they were too small to be thirds (the other percents with decimals).
Students were eager to share their thoughts about what they learned about fraction circles and percents:
- Fractions and percents are the same because the pieces look the same.
- 1/4 is the same as 25% and 2/8
- I don’t get why the eighths end in .5.
- The percents all can be fractions.
- 1/8 is 12.5% because it’s half of 25%
Finally, I asked students to solve a percent problem (now that they’ve all realized that fractions and percents can be used interchangeably). I gave them the m & m problem from this set of percent problem cards. The only direction I gave was that they had to solve the problem using some representation of the percent in the problem before they wrote any numbers.
My bag of M&M’s had 30 candies inside. 40% of the candies were brown. How many brown candies is that?
While this was problematic at first, students looked at their fraction circles and percent cards and realized they could use four of the tenths since each tenth was the same as 10%. Most students needed just one “least helpful” question to get on the right track: Where do the 30 m & m’s belong in your representation?
Most groups were able to make sense and persevere to solve the problem correctly, and explain why they “shared the 30 m & m’s equally among the ten tenths in the fraction circle” and why they “only looked at four of the tenths because that’s the same as 40%.”
My beliefs that were reinforced with this lesson:
- We can’t assume understanding from correct answers alone. We need to listen to students reason through problematic situations.
- Students really want to share their thinking when they realize that someone is really interested in hearing it.
- Students crave understanding. They really want to make sense.
- Procedures are important, but not at the expense of understanding.
- Empowering students by allowing them to build their own understanding and allowing them to make connections allows students to feel comfortable taking risks in problem solving.
Please take a look at Jenise Sexton’s recent blog about percents with 7th grade students for some fantastic ideas about students using number lines and double number lines to solve percent problems. It’s SWEET!
Empowering Students with In-N-Out Burger
The following is a reflection on a 3-Act task I modeled for an 8th grade teacher last week. The 3-Act is In-N-Out Burger from Robert Kaplinsky and the plan I followed I completely stole from the amazing @approx_normal ‘s blog post on her work with the same 3-Act with administrators last year.
This past Thursday was the day we agreed on to model the lesson. So, this group of 8th grade students, who have never even seen me before, are wondering who this guy is that’s about to teach their class. And, just as planned, they were giving me weird looks when I showed them the first cheeseburger picture and asked them what they noticed. I believe one of them even asked, “Are you a teacher?”
Fast forward through to the “What do you wonder?” piece and the questions were amazingly well thought:
- “How much weight would you gain if you at that whole thing (100×100 burger?)”
- “How much do the ingredients cost for it (100×100 burger)?”
- How much does it (100×100 burger) cost?
- “Why would someone order that (100×100 burger)?”
- “Did someone really order that (100×100 burger)?”
- “How long did it take to make the (100×100 burger?)”
There were just a couple more, and they all came up very quickly. The students were curious from the moment we started the lesson. They are still working on precision of language. The parentheses in their questions above denote that this phrase was not used in the question, but was implied by the students. We had to ask what “it” or “that” was periodically throughout the lesson as they worked and as time went on, they did become more consistent.
The focus question chosen was:
- How much does it (the 100×100 burger) cost?
Students made estimates that ranged from $20 to $150. We discussed this briefly and decided that the cost of the 100 x 100 burger would be somewhere between $20 and $150, and many said it would be closer to $150 because “Cheeseburgers cost like $1.00, and double cheeseburgers cost like $1.50, so it’s got to be close to $150.” That’s some pretty sound reasoning for an estimate by a “low” student.
As students began Act 2, they struggled a bit. They weren’t used to seeking out information needed, but they persevered and decided that they needed to know how much a regular In-N-Out cheeseburger would cost, so I showed them the menu and they got to work.
I sat down with one group consisting of 2 boys (who were tossing ideas back and forth) and 1 girl (Angel) who was staring at the menu projected at the front of the room. She wasn’t lost. She had that look that says “I think I’ve got something.” So, I opened the door for her and asked her to share whatever idea she had that was in her head. She said, “Well, I think we need to find out how much just one beef patty and one slice of cheese costs, because when we buy a double double we aren’t paying for all of that other stuff, like lettuce and tomato and everything.” The boys chimed in: “Yeah.” I asked them how they would figure it out. Angel: “I think we could subtract the double-double and the regular cheeseburger. The boys, chimed in again: “Yeah, because all you get extra for the double double is 1 cheese and 1 beef.” “Well done, Angel!” You helped yourself and your group make sense of the problem and you helped create a strategy to solve this problem! Angel: (Proud Smile)!
We had to stop, since class time was over. Other groups were also just making sense of the idea that they couldn’t just multiply the cost of a cheeseburger by 100, since they didn’t think they should have to pay for all of the lettuce, tomato, onion, etc.
They came back on Friday ready to go. They picked up their white boards and markers and after a quick review of the previous day’s events and ah-ha moments, they got to work. Here is a sample after about 15 minutes:
Many groups had a similar answer, but followed different solution pathways. I wanted them to share, but I also wanted them to see the value in looking at other students’ work to learn from it. So I showed this group’s work (below-it didn’t have the post-its on it then. That’s next.). I asked them to discuss what they like about the group’s work and what might make it clearer to understand for anyone who just walked in the classroom.

Here’s what they said:
- I like how they have everything one way (top to bottom).
- I like how they have some labels.
- I’m not sure where the 99 came from. Maybe they could label that.
- Where’s the answer…
During this discussion, many groups did just what @approx_normal saw her administrators do when she did this lesson with them. They began to make the improvements they were suggesting for the work at the front of the room. It was beautiful. Students began to recognize that they could make their work better. After about 5 minutes, I asked the class to please take some post-its on the table and do a gallery walk to take a close look at other groups’ work. They were to look at the work and give the groups feedback on their final drafts of the work using these sentence starters (again, from @approx_normal – I’m a relentless thief!):
- I like how you. . .
- It would help me if you. . .
- Can you explain how you. . .
Some of the feedback (because the picture clarity doesn’t show the student feedback well):
- I like how you showed your work and labeled everything.
- I like how you broke it down into broke it down into separate parts.
- It would help me if you spaced it out better.
- I like how you explained your answer.
- It would help me if it was neater.
- I like how you explain your prices.
- I like how you wrote your plan.
- I like how you explain your plan.
- I like how you told what you were going to do.
- Can you explain how you got your numbers.
- I like how you wrote it in different colors.
- It would help me if you wrote a little larger.
Some samples with student feedback:
Not only was the feedback helpful to groups as they returned to their seats, it was positive. Students were excited to see what their peers wrote about their work.
Now for the best part! Remember Angel? As she was packing up to leave, I asked her if her brain hurt. She said, “No.” After a short pause she added, “I actually feel smart!” As she turned the corner to head to class, there was a faint, proud smile on her face. Score one for meaningful math lessons that empower students.
Please check out the websites I mentioned in this post. These are smart people sharing smart teaching practices that are best for students. We can all learn from them.
So…Have You Always Taught Math This Way?
I’ve been asked this question several times over the past 15 years or so. Most recently at a workshop I facilitated for middle school teachers. The short answer is no. My teaching has evolved. I strive to improve my practice every day. Below, is my response to the group of middle school teachers.
When I first started teaching, I used what I learned in college about teaching mathematics – you know . . . using manipulatives, group work, classroom discussions. All of those things that I still use today. But, when things didn’t go the way I anticipated, I seemed to always fall back on the way I learned which was primarily stand and deliver.
At the end of my first year, I spent some time in my room, at my desk and wrote down all of the changes I wanted to make and how I planned to make them. This was probably the best idea I ever had! Throughout the summer I reread that list and, when necessary, created things that would help me reach my goals. I didn’t reach them all, but the next year was much more successful. Couple that with the summer PL that I took and the way I was teaching math was really beginning to change.
One of the first changes I made was to incorporate children’s literature into my lessons. One of the PL’s I took that summer was a Marilyn Burns workshop where we learned that there are a tremendous number of books with mathematical connections. We learned how use the books to introduce mathematical concepts and problem solving, how to ask better questions, and one of my big “take-aways” was to listen more!
Over the years, I’ve continued to look at literature as a place to begin lessons. And all was going well, but I still wasn’t getting the the amount of buy-in from my students that I wanted. I was excited about the math, but they weren’t. Then, one morning, I was riding to work with my wife, Kim. We were listening to a morning radio show in Atlanta on 99x called the Morning X with Barnes, Leslie, and Jimmy. On that morning, November 10, 1999, Jimmy was laughing about a news story that he couldn’t wait to share. As he was reading, I was scrambling to write it all down! The story went like this:
Earlier this morning a man held up a GA-400 toll booth. His stolen getaway car broke down and he is now on the run with a 58 lb. bag of quarters.
When I got to school, I turned on my computer, printed the story out on a transparency with a picture of some quarters and put it on the overhead. Here’s a sample of what happened:

Several students as they entered the classroom: Mr. W., what’s that on the overhead?
Me: I heard that on the radio this morning and wanted to know what you all thought and if you had any questions.
Multiple student responses: “Oh, ok.” “That guy is stupid.” “What kinds of questions do you want?
Me: Whatever questions come to mind. You can write your thoughts and questions in your journal.
What I got from these 5th grade students at the beginning of class amazed me. They were totally engaged in the problem. The problem context had them so curious, they wouldn’t let go.
Some of their questions:
- How many quarters is that?
- How much money is that?
- How tall would a stack of 58 lbs of quarters be?
- How far could you run with a 58 lb bag of quarters?
- How big is the bag of 58 lbs of quarters?
- How long would a trail of 58 lbs of quarters be if they were laid end to end?
This one context from a morning radio show kept my students focused on the mathematical concepts of weight, length, decimal computation, and time for over a week. More questions came up as new ones were answered. They had developed not only a curiosity, but an intellectual need to know.
This is what I had been searching for. A context that engaged my students in mathematics so deeply, that they wanted to figure out the answers to their own questions.
It wasn’t easy to find stories like this back then. But now, they’re everywhere. Just Google bizarre news stories. Since then I’ve learned, along with a whole host of others (check out some of the people I follow), that I can create these contexts using all sorts of media to get the same results (3-Act Tasks).
Below is a copy of the original context I used with my students. The image has changed over the years, but it is essentially the same document. And it works just as well today as it did 15 years ago! I just wish I had a recording of the news story! If you decide to use this, please share your experience. I’d love to hear about it!
Real Math Homework and Real Learning
Had a great night the other night with my (almost) 14 year old son. Connor had some math homework (Pythagorean Theorem worksheet from an outdated math series) and I was just looking over his work, making sure he understood the concept. He was coming along ok, I guess, so he finished up and sat on the couch to veg. for a bit.
Now, at first I thought what happened next was fate, but the more I think about it my subconscious probably took over. I checked my email and saw one from earlier in the week that I wanted to look at. It was from Dan Meyer’s blog and had a couple of links that I wanted to check out. After about 20 minutes of looking at some stuff I hadn’t seen before– including Estimation 180 (great site by the way), I stumbled upon Dan Meyer’s Taco Cart Problem again and began to grin.
Since I was on the couch with Connor by now, I showed him the video. When it ended abruptly, he said, “THAT’s IT!” I asked what was wrong. He said, “I want to know who gets there first.” We started to talk about it and maybe 20 minutes passed. After realizing this was difficult to do with the limited resources we had on the couch, he asked, “Can we go sit at the table and work this out? These numbers are too big.” I said, “SURE!” (but in a subdued voice so as not to sound “giddy” in front of my teen-aged son).
We sat there for a while talking about what he needed to know. He knew he needed to know how far each person needed to travel, but didn’t make a connection about what he knew about the Pythagorean Theorem to solve the problem. Yes, problem solving should be at the heart of every lesson! He hadn’t been introduced to any ideas about distance and rate, but he knew he needed to know how fast they walked. We talked about the relationship of distance, rate, and time and how these relationships can be use to find solutions to problems like this one.
After a little discussion and a lot of questions, Connor got to work. He stumbled with some of the fraction “mechanics,” but with a little questioning, came through just fine. Connor did more thinking during this task than I’ve witnessed him doing in a long time. He was engaged from the start and he would not stop until he figured it out. This is what students need to do all day in math class!
At the end, it was beautiful! He not only solved the problem, but when I asked where the cart should be for both people to get there at the same time, he was ready to go. He marked a new spot, and figured out the new distance. We had to set it aside, though, because it was getting late. He wants to see how close his placement of the taco cart is for the two guys to get there at the same time. We’ll be looking at it again over the weekend!
Kim, my beautiful bride, stopped at the table and asked what he was doing. He told her, then she asked him if he finished his math extra credit (he doesn’t really need it – it’s just improving his grade, not really improving his understanding of mathematics). I found it a bit humorous because he was learning more doing this problem, than by doing the extra credit sheet of 19 naked equations. Context and comprehension mean everything in mathematics!
Just before he went to bed, I asked him what he thought about the taco cart problem. He said he wished he got to do those kinds of problems at school instead of the “stupid problems he gets in class.”
Connor just recreated his thinking through the Taco Cart problem below using the Educreations App. Enjoy!








