Learning

I Didn’t Know What I Didn’t Know…

Let me just start with this.  If you live in Georgia, say within a 2 hour drive to the UGA Griffin campus, seriously consider joining the Masters’ or EdS program.  I’m in my first semester.  It’s amazing!  ‘Nuff said.

Maybe it’s just me… I thought I understood everything I needed to know about fraction equivalence… until this week.  If you get to the end and think, “Oh, I already knew that!” I apologize.  This is post is really for me to reflect a bit.  If it helps anyone else make sense of fractions…well that’s just gravy!

It all started with an assignment for one of my graduate classes. The assignment was to read Chapter 3 from Number Talks Fractions, Decimals, and Percents by Sherry Parrish and reflect on one of the big ideas and the common misconceptions connected to those big ideas.  I chose to reflect on fraction equivalence.

In the section on equivalence, Dr. Parrish talks about how students want to take fractions like 1/4 and multiply by two to get an equivalent fraction of 2/8. This misconception may be fostered by teachers who wish to make equivalent fractions easy for their students to remember. This is never a good idea!  Because really… if you multiply 1/4 by two, that means you have 2 groups of 1/4.  And 2 groups of 1/4 gives you 2/4 and 1/4 can’t be the same as 2/4.

What I learned next came from a phone conversation I had with Graham Fletcher about 15 seconds after I finished reading the chapter.  Sometimes I just think he knows when I’m learning some math and gives me a call.  He had a question about equivalent fractions. Over the course of about 45 minutes talking on the phone, I think we both deepened our understandings about what makes two fractions equivalent.

Take the rule of multiplying the numerator and the denominator both by the same number to make an equivalent fraction.  If we look at 1/4 and multiply the numerator and denominator by two to get 2/8, we get an equivalent fraction, but this isn’t necessarily the whole story.  To really understand fraction equivalence, I had to be asked to dive a little deeper. Graham asked me to dive deeper.  As we talked, multiplying by one came up, then the multiplicative identity.  These ideas definitely strengthened my understanding of fraction equivalence.

I thought I now had a deep understanding of fraction equivalence.  But wait, there’s more.  This is the best part.  I went to class this past Saturday and Dr. Robyn Ovrick gave us this:

IMG_9381

We were asked to fold the paper as many times as we wanted as long as all of the sections were the same size.  Some of us folded once (guilty – I hate folding almost as much as I hate cutting).  We shared our folds and Robyn recorded what several of us did on the smart board.  Then she asked what we noticed.  This is where everything came together for me.  I tried to share my thoughts but I don’t think I was very successful.  I was really excited about this.  Here is my (1 fold) representation of an equivalent fraction for 1/4:

IMG_8970

For my example, someone said the number of pieces doubled, and at this point (my eyes probably almost shot out of my head) I thought, but the size of the pieces are half as big.  I’m usually pretty reserved and quiet, but this was too much.  So, with a lot of help from colleagues in class who know me a bit better than the others it all came clear to me.  We visually made equivalent fractions, but connected the visual to the multiplicative identity and even explained it in the context of paper folding.

Here it is.

The original paper shows 1/4.  When we fold it in half horizontally, we get 2 times as many pieces and the pieces are half the size.  This can be represented here:

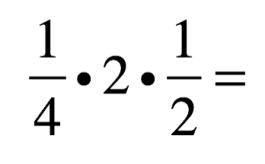
Screen Shot 2017-10-08 at 8.22.03 PM

The 1/4 represents the original fraction. The 2 shows that we got twice as many pieces, and the 1/2 shows that each of those pieces is half the size.  With a little multiplication and the commutative property we can get something that looks like this:

Screen Shot 2017-10-08 at 8.26.14 PM

Knowing that two halves is one whole is definitely part of this understanding, but seeing where it can come from in the context of paper folding allows an opportunity for a much deeper understanding. The numerator tells that there are twice as many sections as before and the denominator (really the fraction 1/2) says that the pieces are now half the size.  We looked at another example of how someone folded 1/4 (someone who folded 8 times!) and noticed that it worked the similarly – we got 8 times as many pieces and the pieces were each 1/8 the size of the original.  I don’t think anyone thought it wouldn’t work similarly, but it sure is nice to see your ideas validate something you thought you really understood before waking up that morning!

I’m still thinking about this and I keep making more connections.  This morning, in a place where I think I do my best thinking (the shower!), I realized that this is connected to the strategy of doubling and halving for multiplication.  I’ll leave you with that.  Time for you to chew.

 

 

 

 

Revisiting 3-Act Tasks

My lessons never stay the same.  They’re always evolving.  Recently, I’ve taken a look at some 3-Act Tasks I created and I noticed:

  • Some of the tasks are lacking an act.
  • Others have resources that no students ask for (at least students that I’ve worked with).
  • The quality is low (shaky camera, point of changes, etc.)

So, I finally had a minute (read 2 days) and revisited each.  Below, you’ll see the tasks I’ve chosen to revisit.  An explanation of the original, what I changed, and why I changed it follows.  If you’d like to skip this and get to the revisited tasks, click here.

Revisited #1 – The Candy Bowl

My very first attempt at a 3-act task was the Candy Bowl task.  I was working in an elementary school at the time and Graham Fletcher had created problem to get 2nd and 3rd grade students reasoning about subtraction by removing the numbers from the problem context.  His context involved the lunchroom and numbers of students in three classes.  We talked on the phone about this for a while and though I liked the problem, I wasn’t crazy about the context.  I sat in my room trying to think of a context that would be a bit more engaging for students to think about.  And the Candy Bowl was created.

 img_4224

It was a good problem, but it really lacked one of the most basic parts of a 3-Act Task… The third act.  The reveal was weak, because it relied on the teacher to give students validation.  The updated version, which had to be done from scratch (apparently whoppers candies are no where to be found anywhere near Valentine’s day), can be found here with all new updated resources for Act 2 and new video including two reveals, depending on which question students decide to tackle.

Revisited #2 – Sweet Tart Hearts

Another one of my early tasks was Sweet Tart Hearts.  I really liked this one from the beginning. There is a huge focus on estimation which allows for students to obtain solutions that are close, but not exact in most cases.  This also allows for the teacher to facilitate a discussion about why answers may not be exact for a variety of reasons.  But again, it really lacked that third act.  The task was good, but the closing of the lesson was weak due to the fact that the students were relying on the “all knowing” teacher to give them affirmation.

screen-shot-2017-02-12-at-2-58-35-pm

Apparently Sweet Tart Hearts are a hot commodity a few days before Valentine’s day.  I went out the other day for a quick run to pick up a bag.  I had to go to 4 stores and finally found a bag (the last one).  I thought it would take about 10 minutes to do this revisit.  Surely the  numbers for the colors would be similar to the last time.  Not only was that not true, but Sweet Tarts changed the orange hearts to yellow!  But, the revisit is all done and I’m very pleased with the new reveal which allows the video to reveal the answer and the teacher to focus students on the reasonableness of their solutions.

Revisited #3 – The Penny Cube

My final revisit is the Penny Cube.  It is probably my favorite task.  I’ve certainly heard more from teachers about this task than any of the others.  I think I got the reveal right on this one.  The problem I found with this task was that I thought students would ask for things that I would want.  The first time I did this task with students, I guided them to the information I had ready for them.  They didn’t care anything about the dimensions of a penny.  They just wanted some pennies and a ruler.  It’s amazing what you learn when you listen to students, rather than try to tell them everything you think they need to know. So, to all of the students out there, Thank you for making your voices heard!

screen-shot-2017-02-12-at-3-02-06-pm

So, this was the quickest fix.  I just updated the Penny Cube page (all of the coin specifications are still there – in case anyone wants them).

Note:  In this post I share how I changed my approach to teaching the Penny Cube task. 

So, it took a few days, but I’ve revisited some tasks that have been bugging me for a while and I hope it’s for the best.  I know I’ll probably give these another look in the future.  I’ll just need to start in early January to make sure I get the candy I need.

Happy Accidents

When I was growing up in (rural-ish) central New York, we had one TV.  We received 5 local stations through the antenna on the roof (abc, nbc, occasionally cbs if the wind was blowing just right, then Fox came along, and a pbs station).  This was a time when TV programming on the major networks actually ended at about 1:00 a.m. with a video of the American flag waving in the wind and the national anthem playing.  When that was over, there was nothing on TV but static.  This is something my kids can’t imagine. Not that they watch regular TV that often anyway (YouTube, Vimeo, etc.), but every time they turn it on, there are at least 100 shows to choose from on 4 TVs.

This wasn’t the case for my siblings and me.  Usually, the first person in the living room got dibs on what show was on or there had to be a “discussion” to figure out what everyone would watch.  Sometimes this ended in the TV being turned off by Mom or Dad with a “suggestion” that we go outside and get some fresh air.  Other times, we would decide to figure it out on our own and end up on the local PBS station watching a man with a huge perm (this was the 1980s) paint beautiful scenes in about 25 minutes.

download

We (my 5 siblings and I) were all in awe while we watched Bob Ross paint wonderful paintings while talking to us (the viewers) about everything from his pet squirrels to painting techniques.  And at the end of every episode I felt like I could paint just like Bob Ross!  I never tried, but I felt like I could!

Recently, my kids have discovered the talent and wonder of Bob Ross through YouTube and Netflix. They love his words of wisdom:

  • “Just go out and talk to a tree.  Make friends with it.”
  • “There’s nothing wrong with having a tree as a friend.”
  • “How do you make a round circle with a square knife?  That’s your challenge for the day.”
  • “Any time ya learn, ya gain.”
  • “You can do anything you want to do. This is your world.”

And I love that they love these words of wisdom.  You can find more here.

For Christmas this year, my son and I received Bob Ross T-shirts.  Connor’s has just an image, while mine has a quote as well:

img_2892

Bob Ross was referring to painting when he said these words; “In painting there are no mistakes, just happy accidents.”  In other words, when you paint your mountain the wrong shape, treat it as a happy accident.  It can still be a mountain, there may just end up being a happy tree or a happy cloud that takes care of your happy accident.

I think it works for math class, too.  Recently, I modeled a Desmos lesson for a 7th grade teacher.  The students had been working with expressions and equations but were struggling with the abstract ideas associated with expressions and equations.  The teacher and I planned for me to model Desmos using Central Park to see how students reacted to the platform (this was their first time using Desmos) and how I managed the class using the teacher dashboard.

During the lesson, there was a lot of productive struggle.  Students were working in pairs and making mistakes happy accidents.  They were happy accidents!  Because students kept going back for more.  At times there was some frustration involved and I stepped in to ask questions like:

  • What are you trying to figure out?
  • Where did the numbers you used in your expression come from?
  • What do each of the numbers you used represent?
  • Before you click the “try it” button, how confident are you that the cars will all park?

The last question was incredibly informative.  Many students who answered this question were not confident at all that their cars would all park, but as they moved through the lesson, their confidence grew.

One of the best take-aways the teacher mentioned during our post-conference was  when she mentioned a certain boy and girl who she paired together so the (high performing) girl could help the (low performing) boy.  The exact opposite happened.  The girl was trying to crunch numbers on screen 5 with little success.  The boy just needed a nudge to think about the image and to go back to some previous screens to settle some ideas in his mind before moving ahead with his idea that the answer is 8.  Then, he got to expain how he knew it was 8 with the picture, conceptually, to his partner.  The teacher’s mistake happy accident was in believing her students would always perform a certain way.  When students are engaged in tasks that are meaningful, they tend to perform differently than when they’re given a worksheet with 30 meaningless problems on it (the norm for this class before Desmos).  Ah-has all around and the “low student” shows that he knows more than the teacher thinks.

The icing on the cake?  Several students walking out of the classroom could be heard saying, “That was cool.” or “That was fun.”

screen-shot-2017-01-04-at-9-53-10-am

Let’s treat math mistakes as happy accidents, something to learn from and problem solve our way through.  When students (all humans) make a mistake, synapses fire.  The brain grows (More on this from Jo Boaler here).  What we do as teachers from this point, determines how much more the brain will grow.  If we treat student mistakes as happy accidents, perhaps their brains will grow a bit more than if we continue to treat mistakes in the traditional manner.

Let’s hear it for Bob Ross.  He probably never thought his words of wisdom about painting would be translated to the math classroom.

Now, go make friends with a math problem.

 

 

 

Georgia Math Conference 2016

For the second year in a row, I had the privilege and honor to give an ignite talk at the Georgia Math Conference (Last year’s talk can be found here.)  What makes ignite talk sessions great is that you get a taste of what several speakers are passionate about and you get to walk away with at least one ember of at least one of those talks beginning to burn in you!

Special thanks to Graham Fletcher for putting this all together (in pre and post production!).  Graham is top notch, “for sure” (Must be a little of my inner Canadian there).

The featured speakers this year in the order of their talk:

Me (@mikewiernicki) – I didn’t ask to go first. 🙂


<p><a href=”https://vimeo.com/190360814″>Mike Wiernicki – Ignite Talk (GCTM 2016)</a> from <a href=”https://vimeo.com/user21534889″>Graham Fletcher</a> on <a href=”https://vimeo.com”>Vimeo</a&gt;.</p>

Katie Breedlove (@KatieBreedlove)


<p><a href=”https://vimeo.com/190362489″>Katie Breedlove – Ignite Talk (GCTM 2016)</a> from <a href=”https://vimeo.com/user21534889″>Graham Fletcher</a> on <a href=”https://vimeo.com”>Vimeo</a&gt;.</p>

Jenise Sexton (@MrsJeniseSexton)


<p><a href=”https://vimeo.com/190364708″>Jenise Sexton – Ignite Talk (GCTM 2016)</a> from <a href=”https://vimeo.com/user21534889″>Graham Fletcher</a> on <a href=”https://vimeo.com”>Vimeo</a&gt;.</p>

Karla Cwetna (@KCwetna)


<p><a href=”https://vimeo.com/190381786″>Karla Cwetna – Ignite Talk (GCTM 2016)</a> from <a href=”https://vimeo.com/user21534889″>Graham Fletcher</a> on <a href=”https://vimeo.com”>Vimeo</a&gt;.</p>

Carla Bidwell (@carla_bidwell)


<p><a href=”https://vimeo.com/190286621″>Carla Bidwell – Ignite Talk (GCTM 2016)</a> from <a href=”https://vimeo.com/user21534889″>Graham Fletcher</a> on <a href=”https://vimeo.com”>Vimeo</a&gt;.</p>

Brian Lack (@DrBrianLack)


<p><a href=”https://vimeo.com/190415942″>Brian Lack – Ignite Talk (GCTM 2016)</a> from <a href=”https://vimeo.com/user21534889″>Graham Fletcher</a> on <a href=”https://vimeo.com”>Vimeo</a&gt;.</p>

Graham Fletcher (@gfletchy) – The great Emcee’s talk is available elsewhere.  I’ll find it and link it asap.

 

 

Unlikely Students in Unknown Places

I recently got back from Santa Fe.  I was attending a conference there for a few days last week and afterward, I drove to El Paso to visit my brother’s family (he’s currently stationed in the middle east so I didn’t get to see him – unless you count face time) for a day before flying home.

Let me preface this story by saying that we all probably have a story similar this, but how we handle it can be a possible game changer.

Somewhere on my long drive, I stopped at a fast food restaurant to grab a quick bite.  So, I went inside and got in line.  The following outlines the beginning of our interaction as I stepped to the counter:

Cashier:  May I take your order?

Me:  Yes, please.  I’d like a number 2.

Cashier:  Large or medium.

Me:  Medium, please.

Cashier:  (after pushing more buttons than is conceivably necessary to enter my choice of “medium”): Your total will be $6.05.

I dug through my wallet (receipts from the trip and everything) and found that all I had was a $10 bill, so I handed it to her.  She entered $10.00 correctly and the correct change of $3.95 showed up on the little screen.  At just about that point, I remembered that I had a bunch of change in my pocket and said quite enthusiastically, “Oh, wait, I think I have a nickel.”  Who wants to carry around $0.95 in change in their pocket.

The cashier didn’t miss a beat, and said, “So, your change will be $4.00 even.”  I kind of smiled as I continued to look through my change, proud that she had a mental strategy to adjust to the situation and that she seemed quite confident and comfortable using it in this situation.

Unfortunately, I didn’t have a nickel, but I still didn’t want change falling out of my pocket into the depths of the rental car, never to be seen by me again.  So, I told her, “Oh, I’m sorry, I don’t have a nickel, but I do have a dime.”

As I handed her the dime, I saw her face morph from a confident smirk to a confused, almost terrified look of despair .  I had just taken her from a mathematical point of “Yeah, I can do this math stuff.  I may not use the computer for the rest of my shift” to “Holy $#!+, what the #=|| just happened!”

I went into math teacher mode and waited patiently for her to begin breathing again.  And then I waited for her begin thinking.  She adjusted my change with my introduction of the idea of a nickel, why not a dime? After what seemed like 5 minutes (probably more to her), it was painfully obvious to all around that her anxiety in this situation was taking over her ability to tackle this problem. So, I tried to think of a “least helpful question” to ask.  Now I put myself on the spot.  If she only knew that we were both now feeling some of this pressure.

So, I finally asked her my question and she gave me the correct change within a few seconds.  She smiled as she gave me my change and my new “unknown” student and I parted ways.  I know I felt good about helping someone develop a strategy outside of the classroom.  I hope she had a similar feeling about learning to make sense (no pun here) of making change.

Being a math teacher is a 24-7 job sometimes and we can find our students anywhere – even in a fast food restaurant in New Mexico!

What you would have asked the cashier in this situation.  I’d love to hear what your “least helpful” question would have been. No pressure, take as long as you like.  No one is waiting in line behind you!

Feed the hungry!

Oh, here’s my question:  “If you could change the dime into some other coins, what would you change it for?”

Math: A Fun After Homework Activity

All week long I’ve been asking Connor, my 9th grade son, what he has been working on in coordinate algebra.  Here’s a snippet of a recent conversation:

  • Me:  So, Connor, what have you been working on in your coordinate algebra class?
  • Connor:  We’ve been graphing.
  • Me:  Graphing what?
  • Connor:  Graphing different lines.
  • Me:  What kinds of lines are you graphing?
  • Connor:  Ummmm…
  • Me:  Are they linear functions.
  • Connor: Yeah, there are linear functions, but we also do curves…
  • Me:  Like what kind of curves?
  • Connor: Umm… exponents
  • Me:  Ok.  Anything else?
  • Connor: Umm…
  • Me:  Hey, I want to show you something. . .

Versions of this conversation happened several times this week.  Due to soccer practices, games, homework, and Life in general, we never got much past Connor’s last “Umm…”

Until yesterday!  The conversation changed a bit:

  • Connor:  We did something cool in class today.
  • Me:  Oh, yeah?  What was it?
  • Connor:  We had to build a picture using graphs of different lines.  We built a shamrock.
  • Me:  That’s what I’ve been meaning to show you all week.  Go grab my laptop.
  • Connor:  (playing game of war on an ipad) But I finished my homework.
  • Me:  Just take a look at this for a few minutes and see what you think.
  • Connor: (heavy sigh)

Enter Des-Man from Desmos.  Once he had gone through the tutorial, he was hooked. . . for a while!  He engaged in this for about 2 1/2 hours.  When he wanted to make something happen, but didn’t know how, he would come to me and ask.  We’d figure it out together.  The best part of this whole experience was when he realized he knew how to create something on his own and went to his math work from class as a reference.

Fast forward to 2 1/2 hours later, when Connor finished his Desman.

Des-man

 

 

 

 

 

 

 

To see the picture in detail along with the equations Connor used to create this graph, click Connor Face Graph.

It didn’t stop there.  I had some tabs open and clicked on one with the In-N-Out Burger task from Robert Kaplinsky.  He was curious enough to work through it even after all of the Des-man work.  So, I showed him more by clicking on the Open Middle tab (also from Robert Kaplinsky).  I selfishly pulled up the task that I wrote in collaboration with Graham Fletcher called The Greatest Difference of Two Rounded Numbers.  After making sense of the problem, and a lot of eye opening moments that led to phrases like “Oh, I can make it larger!” He got what he thought was the final answer and we validated his reasoning by clicking on the answer.  A slight smile!

So, we’re looking at close to 3 hours of after homework math investigation that ranged from rounding numbers to graphing equations, and solving problems.  Sounds like a great evening to me.  Great conversations and fun while learning and reinforcing mathematics understanding!  What could be better?  Talking Math With Your Kids – High School Edition.

Feed the hunger of all ages!

More with Connor:  Real Math Homework and Real Learning

Math Students are Bleeding Out!

Let me explain.  There’s a math epidemic (remember Ebola 2014+).  Students are bleeding out from the gashes of their misconceptions of mathematics.  The lack of teaching conceptual understanding along with sacrificed opportunities to make mathematical connections is the double edged sword.  This is an epidemic, and some teachers, school systems and educational leaders are treating it like it’s a tiny scratch, instead of the pervasive threat to mathematical achievement that it is.

Here’s a familiar scenario:  A school’s test scores come back after the spring testing season (or mid-terms).  The scores show little growth from the previous year in the area of mathematics, and any change is not in a positive direction.  The knee-jerk reaction to the valid question, “What can we do to fix this?”  is to look for programs and technology that will fix the problem.  These are the same individuals who, way back in August, looked us all in the eye and, with the greatest of sincerity, reminded us that the single most important factor determining student success is the quality of the teacher.  Not new programs.  Instead of growing the quality of teachers, we get programs that:

  • push speed over comprehension (imagine if we taught reading this way).
  • define fluency based on digits rather than efficiency, flexibility, and accuracy.
  • use technology to separate us from our students when we know that what we really need is to spend more time listening to them and creating an interactive classroom with technology as a support for this human interaction
  • are essentially Band-Aids

I often hear the phrase “back to the basics” in times like these.   I’ve heard parents, administrators, and even a few teachers say this.  I think everyone would agree that “back to the basics” should mean that students become computationally fluent.   The idea of going back to this implies that we were doing something right before.  And we all know that’s not true.  After all we have generations of adults who are not computationally fluent and/or have extreme math anxiety.  And how did that happen?

Answer 1:  Timed tests.  My sixth grade teacher called them speed tests.  We did them every day, right after lunch.  (I was never in the top 10).

Answer 2:  Algorithms memorized by students with no understanding, presented by teachers with little understanding other than from a teachers’ edition.

Answer 3:  Little or no real problem solving.  Naked computation all around.  No wonder students were turned off by mathematics!

Answer 4:  No interaction.  Math is a social activity.  If you talk to any engineer, designer, architect, mathematician, statistician, etc.  They aren’t doing their work in an office silently sitting in rows.  They’re constantly talking to one another about the mathematics they’re using.  The idea that all of us are smarter than one of us makes so much sense in the real world and it should make sense in the classroom as well.

If we went back to teaching math like we did 20-30 years ago (I think that’s what some of these folks were implying when they said “back to the basics.”  We’d still be in the same boat.  Anyone ever watch How old is the shepherd?.  That was popularized over 20 years ago and the results haven’t changed.  Going back is not an option.  Building fluency is.

So what do we need to do in math classrooms?  I have a few ideas to stop the bleeding and these are certainly not original to me.

keep calm

  1. Apply pressure to the wound. Give up on the ineffective treatment, not the patient.  Apply pressure to stop the bleeding.  Focus on tasks and activities that build number sense.  Number Talks, Math Talks, Estimation 180, Visual Patterns any or all of these can be put in place at any level.  And the best part is, students can easily be trained to begin to apply the pressure themselves.  They have the power to stop the bleeding!
  2. Close the wound. This can only happen with stitches.  And it takes time to get the hang of it.  The wound has to be closed with the thread of understanding.  We can’t understand for them, so the wound has to be closed with the help of the students.  The students create this thread as we stitch and we can’t do it without them.  How do they create this thread of understanding?  We have to stop telling so much and instead “be less helpful.”  If we tell students too much, the thread breaks.
  3. Treat any symptoms that may show up after the initial treatments above:

Symptoms

 Name

Treatment

Students may begin to rely on rote procedures with no foundational understanding

Sometimes unintentionally caused by parents & other adults trying to help.

 Misconceptionitis Identify the misconception(s) and re-build understandings using the CRA (Concrete Representational Abstract) model

Students are finding unreasonable solutions to tasks & problems and they often seem unaware; clueless

 Unreasonableness

This is often attributed to students just not thinking enough.  Treatment should include a DAILY diet rich in estimation – prescribe www.estimation180.com

Students count (often on fingers when computing or rely on a calculator for the simplest of calculations and even then, they can get incorrect answers.

 Influencia

This is often diagnosed along with unreasonableness (see above).  Its roots lie in naked computation and memorization of facts rather than allowing students to build strategies and practice those strategies until they become fluent.  First, counting strategies are the lowest level strategies.  Students need to build more efficient strategies by exercising with  investigations of number relationships through number talks, math talks, and strategy building.  Stop giving speed tests.
Students have strategies for computation, but are not applying them in problem solving situations No Solvia

Students need a heavy dose of problem solving every day.  This must involve students engaging in the Big 8 Standards for Mathematical Practice.  Problem solving tasks every day.  Hydrate often with student reasoning.  Adopt the classroom mantra: “The answer isn’t good enough.”

Begin new concepts with a problem before any formal instruction on the topic.  See what students can do before assuming what they can’t do.

I’m a teacher and I know many of you reading this are the choir that need no preaching to.  If you’re interested in saving the patient, stopping the bleeding, and raising math achievement, click on some of the links in this post.  There’s so much to learn from those smarter than me.  Also check out #MTBoS on Twitter.  Lots of math goodness from the best out there.

Click here and here to learn more about strategy development.  Great stuff from www.nzmaths.co.nz!

The Penny Cube

I just finished a 5th grade 3-Act task called Penny Cube that I created last spring.  I tried it then, but just to get some feedback from students and see what I might need to change about how the task should be presented.  Now, after completing this task with two groups of students (at two different points in the year), I’ve learned three things:

  1. Students see a video and notice a bunch of things that teachers don’t even realize are there.
  2. The curious questions students ask first are often “why” questions.
  3. There’s no way to predict everything a group of students might wonder.

I’ll take this reflection from the beginning.  First, I let students know that I was going to show them a video clip.  I also told them that I was going to ask them what they noticed when it was finished playing.  I gave students a chance to brainstorm ideas about what they could do to make sure they would be able to share what they noticed once the clip had finished playing.  Their ideas were amazing:

  • We could look for expressions (on faces – I found out later that this student was thinking about context.  A person’s facial expression can tell a lot)  Unfortunately, there were no facial expressions in this video.
  • Listen carefully (they might be able to hear something that might give them a clue about what was going on – these students were already expecting a problem situation!)
  • Stay focused on the clip.
  • Take notes.
  • Try to remember as much as you can.

I had never done this before, but after hearing their ideas, I will be using this again.

After showing the video clip for Act 1, I immediately had them talk about what they noticed with their groups.  Then, they were asked to share with the whole group.  Here is what they noticed:

Penny Cube Notices

What’s missing from this picture is the wonderful reasoning given for some of these.  For the last bullet, “container is open in the front,” the student told the class that it was open in front so the pennies could be placed in the container more easily (I never thought they’d see or think about that).  They even began to wonder a bit here – “it might be an expression or it might be counting.”  My favorite, though, is the estimation by the girl who said “it looks like 100 pennies in the stack ($1.00).”  This was particularly interesting to me because of what happened when they were asked to estimate for the focus question.

The wonders were typical from what I usually get from students new to 3-Act tasks, but I handled it a bit differently this time.  Here are their wonders (click here for a typed version of Penny Cube Notices&Wonders):

Penny Cube Wonders

In my limited (yet growing) experience with teaching using 3-Act tasks, I’ve noticed that the wonders are initially “why” questions (as stated in number 2 above).  I told the class that I noticed that the questions they were asking were mostly “why” questions.  I asked them what other words could be used to begin questions.  Rather than trying to steer students to a particular question, I decided to focus the students’ attention on the kinds of questions they were already asking, and guide them to other types of questions.  It didn’t take long!  Within about 5 minutes, students had gone from “why” questions to “how many . . .” and “how much . . .” questions which are much easier to answer mathematically.

The students were then asked to figure out what they needed to solve the problem.  From experience with this task, I knew that most students would want pennies, so I had some ready.  I didn’t give them the Coin Specifications sheet, because no one asked for it.  I did have it ready, just in case.  Every group asked for pennies and rulers.  I wasn’t sure how they would use them, but I was pleasantly surprised.

Here’s what they did:

How many pennies in 2 inches

How many pennies in 2 inches

How many pennies in an inch

How many pennies in an inch

How many pennies fit on a 6 inch edge of the base

How many pennies fit on a 6 inch edge of the base

How many pennies cover base

How many pennies cover base

How many stacked pennies in 2 inches?

How many stacked pennies in 2 inches?

 

 

 

 

 

 

 

 

 

 

 

The students all started in a place that made sense to them.  Some wanted to figure out how many in the stack, so they stacked pennies and quickly realized (as I did when filling the cube) that you can’t stack pennies very high before they start to wobble and fall.  So, they measured smaller stacks and used that info to solve the problem.  Others wanted to find number of pennies along an edge to find how many cover the base, then work on the stacks.  Students were thoroughly engaged.

After three 1 hour classes, students were wrapping up their solutions.  Some groups were still grappling with the number of pennies in a stack.  Others were finished.  A few were unsure about what to do with some of the numbers they generated.  All of this told the classroom teacher and me that there were some misconceptions out there that needed to be addressed.  Many of the misconceptions had to do with students disengaging from the context, rather than integrating their numbers into the context:

  • One group was unsure of whether to multiply  the number of pennies in a stack by 12 (6 inches + 6 inches) or to use 64.
  • Another group found the number of pennies to cover the base and multiplied it by itself to get their solution.
  • A third group found 37 pennies in 2 1/2 inches and was having a difficult time handling that information.
  • A fourth group had come up with two different solutions and both thought they were correct.  Only one could defend her solution.

Eventually, several groups arrived a solution that made sense to them.

Time to share!

I chose one group to share.  This group had a reasonable solution, but their method and numbers were different from many of the other groups, so this is where we were hoping for some light bulbs to begin to glow a bit.

This group shared their work:

20140919145046-3351215

 

 

 

 

 

 

 

 

 

 

I asked the class what they liked about the work.  The responses:

  • The math (computations) are written neatly and they’re easy to follow.
  • I know what their answer is because it has a bubble around it.
  • The question is on it.
  • It’s colorful.

All good.  Now, for the best part:

What questions do you have for this group?  The responses:

  • Where did you get 34?
  • What does the 102 mean?
  • How about the 64?

Any suggestions for this group to help them clarify their work to answer some of your questions?

  • Maybe they could label their numbers so we know what the numbers mean.
  • Maybe they could tell what the answer means too.  Like put it in a sentence so it says something like “6,528 pennies will fit in the container.”
  • Maybe they could have a diagram to show how they got a number like 64 or 34.  I know that would help me (this student had a diagram on his work and thought it was useful).

The light bulbs really started to glow as students began making suggestions.  As soon as a suggestion was made, students began to check their own work to see if it was on their work.  If it wasn’t, they added it.  All of the suggestions were written on the board so they could modify their work one final time.  The best part about this whole exchange was that students were suggesting to their peers to be more precise in their mathematics (SMP 6 – Attend to precision).  And, they really wanted to know what 34 was because they didn’t have that number on their boards (which is why I chose this group).

Now for the reveal!  When I asked the class if they wanted to know how many pennies were in the cube, they were surprised when I pulled up the reveal the video.  I guess they thought I’d just tell them (that’s so 1980’s).  They watched to see how close they were and when the total came up on the screen, many cheered because they were so close!

The students in this class were engaged in multiple content standards over the course of 3 days.  They reasoned, critiqued, made sense, and persevered.  It’s almost difficult to believe that this class was a “remedial” class!

Below, I’ve included a picture of each group’s final work.

20140916143126-1706895 20140916143218-1880868 20140916144859-1652302 20140916143241-1966871 20140916143157-1917874

 

 

 

 

 

 

 

Finally, one of the conversations witnessed in a group was between a girl and a boy and should have been caught on video, but wasn’t.  This group had an incorrect solution, but they were convinced they were correct, so to keep them thinking about the problem, I asked them how many dollars would be equal to the number of pennies in their answer (3,616).

  • Girl:  There are 100 pennies in a dollar.  So 600 pennies is . . .
  • Boy in group: $6.00
  • Girl (after a long pause):  1,000 pennies equals $10.00
  • Boy:  So that’s . . . um. . .
  • Me:  How does knowing 1,000 pennies = $10.00 help you.
  • Girl:  We have 3,000 pennies, so that’s $30.00.
  • Boy:  $36.00
  • Me:  Share with your group how you know it’s $36.00
  • Boy:  Because $30.00 and $6.00 is $36.00
  • Girl:  And the rest (16) are cents.  $36.16!

And they didn’t even need a calculator!

Math really does make sense!

Why use 3-Act Tasks?

The short answer:  It’s what’s best for kids!

If you want more, read on:

The need for students to make sense of problems can be addressed through tasks like these.  The challenge for teachers is, to quote Dan Meyer, “be less helpful.”  (To clarify, being less helpful means to first allow students to generate questions they have about the picture or video they see in the first act, then give them information as they ask for it in act 2.)  Less helpful does not mean give these tasks to students blindly, without support of any kind!

This entire process will likely cause some anxiety (for all).  When jumping into 3-Act tasks for the first (second, third, . . .) time, students may not generate the suggested question.  As a matter of fact, in this task about proportions and scale, students may ask many questions that are curious questions, but have nothing to do with the mathematics you want them to investigate.  One question might be “How is that ball moving by itself?”  It’s important to record these and all other questions generated by students.  This validates students’ ideas.  Over time, students will become accustomed to the routine of 3-act tasks and come to appreciate that there are certain kinds of mathematically answerable questions – most often related to quantity or measurement.

These kinds of tasks take time, practice and patience.  When presented with options to use problems like this with students, the easy thing for teachers to do is to set them aside for any number of “reasons.”  I’ve highlighted a few common “reasons” below with my commentary (in blue):

  • This will take too long.  I have a lot of content to cover.  (Teaching students to think and reason is embedded in mathematical content at all levels – how can you not take this time)
  • They need to be taught the skills first, then maybe I’ll try it.  (An important part of learning mathematics lies in productive struggle and learning to persevere [SMP 1].  What better way to discern what students know and are able to do than with a mathematical context [problem] that lets them show you, based on the knowledge they already have – prior to any new information. To quote John Van de Walle, “Believe in kids and they will, flat out, amaze you!”)
  • My students can’t do this.  (Remember, whether you think they can or they can’t, you’re right!)  (Also, this expectation of students persevering and solving problems is in every state’s standards – and was there even before common core!)
  • I’m giving up some control.  (Yes, and this is a bit scary.  You’re empowering students to think and take charge of their learning.  So, what can you do to make this less scary?  Do what we expect students to do:  
    • Persevere.  Keep trying these  and other open problems.  Take note of what’s working and focus on it!
    • Talk with a colleague (work with a partner).  Find that critical friend at school, another school, online. . .
    • Question (use #MTBoS on Twitter, or blogs, or Google 3-act tasks).  
    • Write a comment below. 🙂

The benefits of students learning to question, persevere, problem solve, and reason mathematically far outweigh any of the reasons (read excuses) above.  The time spent up front, teaching through tasks such as these and other open problems creates a huge pay-off later on.  However, it is important to note, that the problems themselves are worth nothing without teachers setting the expectation that students:  question, persevere, problem solve, and reason mathematically on a daily basis.  Expecting these from students, and facilitating the training of how to do this consistently and with fidelity is principal to success for both students and teachers.

Yes, all of this takes time.  For most of my classes, mid to late September (we start school at the beginning of August) is when students start to become comfortable with what problem solving really is.  It’s not word problems – mostly. It’s not the problem set you do after the skill practice in the textbook.  Problem solving is what you do when you don’t know what to do!  This is difficult to teach kids and it does take time.  But it is worth it!  More on this in a future blog!

Tips:

One strategy I’ve found that really helps students generate questions is to allow them to talk to their peers about what they notice and wonder first (Act 1).  Students of all ages will be more likely to share once they have shared and tested their ideas with their peers.  This does take time.  As you do more of these types of problems, students will become familiar with the format and their comfort level may allow you to cut the amount of peer sharing time down before group sharing.

What do you do if they don’t generate the question suggested?  Well, there are several ways that this can be handled.  If students generate a similar question, use it.  Allowing students to struggle through their question and ask for information is one of the big ideas here.  Sometimes, students realize that they may need to solve a different problem before they can actually find what they want.  If students are way off, in their questions, teachers can direct students, carefully, by saying something like:  “You all have generated some interesting questions.  I’m not sure how many we can answer in this class.  Do you think there’s a question we could find that would allow us to use our knowledge of mathematics to find the answer to (insert quantity or measurement)?”  Or, if they are really struggling, you can, again carefully, say “You know, I gave this problem to a class last year (or class, period, etc) and they asked (insert something similar to the suggested question here).  What do you think about that?”  Be sure to allow students to share their thoughts.

After solving the main question, if there are other questions that have been generated by students, it’s important to allow students to investigate these as well.  Investigating these additional questions validates students’ ideas and questions and builds a trusting, collaborative learning relationship between students and the teacher.

Overall, we’re trying to help our students mathematize their world.  We’re best able to do that when we use situations that are relevant (no dog bandanas, please), engaging (create an intellectual need to know), and perplexing .  If we continue to use textbook type problems that are too helpful, uninteresting, and let’s face it, perplexing in all the wrong ways, we’re not doing what’s best for kids; we’re training them to not be curious, not think, and worst of all . . . dislike math.

More Resources like 3-Act Tasks: