Problem Solving

Hubbub

A partner game for developing student flexibility with number combinations to five and ten (or even 20) that has connections to the first Thanksgiving.

If you teach Kindergarten, this post (and game) is for you! Ok, 1st Grade teachers can use this too, in the beginning of the year, or with more ten frames.

I can’t believe I haven’t written a post about this. I learned about Hubbub about 17 years ago, when I was just starting as a math coach in my district. I heard in mentioned in a video that some Kindergarten students were watching to learn about the first Thanksgiving. Apparently, children played Hubbub at the first Thanksgiving. I jotted down the rules and added a double ten-frame as a score board.

Materials needed:

5 two-color counters per pair of students
Double ten-frames (one per pair) (one per student, if working on composing numbers to 20)
Cubes (10 per student) (20 per student if each child has a double ten-frame)

Rules:

The object of the game is to score 10 points (or 20 points if you use a double ten-frame for each student).
Players alternate shaking and spilling the 5 two-color counters. A player continues their turn (shaking and spilling counters to earn points) until they shake and spill 4 counters of one color and 1 counter of another color.
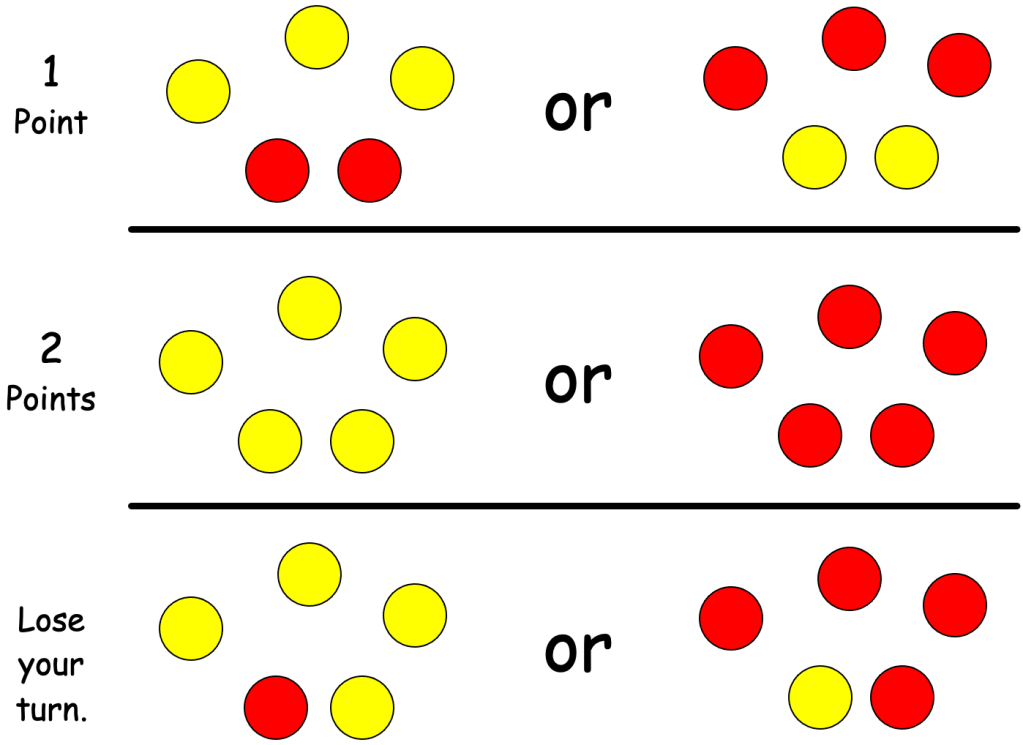
Points are scored according to how the two-color counters land (see scoring sheet linked below):
- If the counters show 3 of one color and 2 of another color, the player earns 1 point.
- If all five counters show the same color, the player earns 2 points.
- If the counters show 4 of one color and 1 of another color, the counters get passed to your partner.
Players keep score by placing cubes on a ten-frame for each point earned. Players never lose the points they earn.

Teaching the Game

This is a partner game. I always model this game with the teacher on the carpet and we talk about the rules of the game, how to toss the counters, and good sportsmanship.

I sometimes use same-different images as an opener to this game. The slides for these can be found below, along with my lesson notes (standards included).

I introduce the two-color counters and then I shake them in my hands and gently drop them on the carpet. The counters will show one of six combinations:

As you can see, the possibilities are grouped by combinations to five (3 yellow and 2 red or 3 red and 2 yellow, etc.)

These combinations have scores/ consequences associated with them.

As we model the game, each time a new combination shows up, we discuss what happens. The scores and consequences for each pair of combinations is shown below.

A players turn only ends if they roll 4 of one color and 1 of another color. This is important, because most games we play with students, players each take one turn after each roll. We continue to model playing the game discussing good sportsmanship and asking questions, like “How many more do I need to get to 10?” “How many points do you have?” “Who has more points?”.

When someone wins – almost always not me – we ask the students if they are ready to play. The teachers pair the students with their partners, and we give them their materials. Students then begin to play and we monitor, asking students questions about combinations to five and 10 as they play. Students get very excited and, since we model it, we often hear students who do not “win” say, “That was a good game, would you like to play again?”

Hubbub Materials

If you use this game, please share your experiences. I’d love to hear how you may have changed the game to suit your students’ needs.

Full disclosure here – I never won this game (17 years of playing) until last week when I went to my wife’s school to teach this to the Kindergarten classes before Thanksgiving break. They took a picture because it was the first time I ever won!

Finding the Greatest Product – 5th Grade Students

This is a lesson from several years ago, that I borrowed from a post from Fawn Nguyen. Her blog post describing how she used it is excellent!

In this lesson, students are given 5 digits and their goal is to find the greatest product without actually doing the computation. The fifth grade students I used this with loved it. We took two days – one day to introduce the problem and a second day to try it again with different numbers, and find patterns. This is a fantastic problem because of the connections to so much more than place value!

Day 1

I started out with the same numbers Ms. Nguyen used in her example on her post. I did this because of time constraints on the first day. PTO performance dress rehearsals can really mess up a plan!

So the students were given the digits 8, 2, 4, 5, and 7. The task was to create two factors that would give the greatest product without actually doing the multiplication.

I asked students to take 90 seconds to think about it, then share their ideas with their groups. The math discussions were incredible. “582 x 47″ is less than hers because 582 x 74 has to be bigger. That one has only 47 groups of 582. This one has 74 groups of 582!” Similar comments/discussions happened at each table.

The students then shared their ideas for the two factors that would make the greatest product as I wrote them on the board:

582 x 74 = 782 x 54 = 872 x 45 =

825 x 74 = 752 x 48 = 752 x 84 =

754 x 82 = 572 x 84 =

I asked students to look carefully at their list and discuss with their tables which two they think should be removed and why. I did remind students that they should base their decisions on mathematical reasoning, not computation.

After about 90 seconds of discussion, I asked each table to identify the problem they think should go. After two tables shared, everyone agreed that these two (in red) should go.

582 x 74 = 782 x 54 = 872 x 45 =

825 x 74 = 752 x 48 = 752 x 84 =

754 x 82 = 572 x 84 =

The students’ reasoning ranged from rounding to doubling and halving to just finding one more on the list that had to be greater. After that, students had to decide from the 6 left, which one would produce the greatest product. Most groups eliminated 2 or 3 more, but they struggled to find 1 because they thought it could go either way (see the green problems above).

Again, due to time constraints and PTO rehearsals, I asked them to choose one. The classroom teacher who was observing, had already found the products of all of the problems on the board. We asked for the products and wrote them on the board to some cheers of “Yes!” and some groans of “No!”

All agreed that it was a fun exercise. I loved it because the students were engaged in several of the mathematical practices, specifically constructing viable arguments and critiquing the reasoning of others This happens in other lessons, for sure, but it seemed more natural here because the disagreement was based on the reasoning used. Since not all students think the same way (and they shouldn’t), there were natural mathematical arguments discussions.

Before I left the classroom, I pulled out my deck of cards and had 5 students choose a number card to generate 5 new digits so that when they finished their PTO performance later in the evening, they could think some more about the math we did in class today. They were asked to come up with a 3-digit factor and a two digit factor that they think would give the greatest product.

Day 2

The next day, we went through the same process (the previous day’s work was on the board for them to refer to). The numbers the students drew were: 2, 9, 6, 7, 8

There were 12 ideas for the greatest product this time.

892 x 76 = 782 x 96 = 982 x 76 =

987 x 62 = 267 x 89 = 762 x 98 =

769 x 82 = 862 x 97 = 872 x 96 =

872 x 69 = 972 x 86 = 962 x 87 =

Again, I asked them to think for 90 seconds on their own, then share their thoughts with their tables about which problems could be eliminated based on mathematical reasoning. After sharing, I asked each table for their thoughts about which should go and why.

Again, the reasoning was amazing. The class, as a whole, came up with reasoning to eliminate 8 of the 12. They’re shown below in red.

892 x 76 = 782 x 96 = 982 x 76 =

987 x 62 = 267 x 89 = 762 x 98 =

769 x 82 = 862 x 97 = 872 x 96 =

872 x 69 = 972 x 86 = 962 x 87 =

The class got into a discussion about which of the remaining should go without prompting because they were so engaged in this problem! The class could not decide, but it was pretty well split between the green problems above.

Some thought it was 862 x 97 because:

“It’s almost 100 groups of 862 and 872 x 96 has one less group of a smaller number, but it isn’t enough.”

The other group countered with:

“We still have almost 100 groups of a larger number. We have one less group, but we have 10 more in each group!”

Again, the teacher was ready with the products and we checked all of the eliminated problems first to justify their earlier reasoning. We heard a few things that really made these two days worth it like: “See, I told you it was about 27,000” and “We were right get rid of that one!” Makes your heart swell up when kids say those things with mathematical confidence!

When we got down to the final two, they were on the edge of their seats! As the final products were revealed, there were no “I told you so’s” or mocking of others. The students really enjoyed the productive struggle of thinking and reasoning about greatest products. The students had a great time, but it wasn’t over yet.

As some in Queen Nguyen’s class, one student noticed a pattern from the work of both days. His explanation is described below:

“I noticed in both problems that the 2 was in the same place (red underline) and that it’s the smallest of the digits we used, so I thought about the largest numbers (digits) and checked to see if they’re in the same place and they are (Blue underline)!”

Another student chimed in with “There’s more. Look, the greatest digit is in the tens place for the second number. The next greatest digit for the first problem is 8 (green underline) and it’s in the hundreds place. For the second problem, the next greatest digit is 7 (green underline) and it’s in the hundreds place, too! And the third? greatest digit is right next to that in the tens place of the first number. And the digit before the smallest is in the ones place of the second number.”

The students were eager to check another set of numbers to see if this pattern they found could actually be a mathematical discovery. They wanted 5 more digits to use to check – they were asking to do more math! Before they left for the day, I found out that some students wondered if the pattern would change if it was a 4 digit times a 3 digit. Guess we’ll have to do another exploration!

All of this stemmed from asking students to reason about multiplication. In the process, all of their ideas were used to build a deeper understanding of multiplication and estimation. As a result, they made an interesting mathematical discovery based on the patterns they discovered and posed a new question to explore!

Thanks, again, to Fawn Nguyen for sharing this problem!

Happy Accidents

When I was growing up in (rural-ish) central New York, we had one TV. We received 5 local stations through the antenna on the roof (abc, nbc, occasionally cbs if the wind was blowing just right, then Fox came along, and a pbs station). This was a time when TV programming on the major networks actually ended at about 1:00 a.m. with a video of the American flag waving in the wind and the national anthem playing. When that was over, there was nothing on TV but static. This is something my kids can’t imagine. Not that they watch regular TV that often anyway (YouTube, Vimeo, etc.), but every time they turn it on, there are at least 100 shows to choose from on 4 TVs.

This wasn’t the case for my siblings and me. Usually, the first person in the living room got dibs on what show was on or there had to be a “discussion” to figure out what everyone would watch. Sometimes this ended in the TV being turned off by Mom or Dad with a “suggestion” that we go outside and get some fresh air. Other times, we would decide to figure it out on our own and end up on the local PBS station watching a man with a huge perm (this was the 1980s) paint beautiful scenes in about 25 minutes.

We (my 5 siblings and I) were all in awe while we watched Bob Ross paint wonderful paintings while talking to us (the viewers) about everything from his pet squirrels to painting techniques. And at the end of every episode I felt like I could paint just like Bob Ross! I never tried, but I felt like I could!

Recently, my kids have discovered the talent and wonder of Bob Ross through YouTube and Netflix. They love his words of wisdom:

“Just go out and talk to a tree. Make friends with it.”
“There’s nothing wrong with having a tree as a friend.”
“How do you make a round circle with a square knife? That’s your challenge for the day.”
“Any time ya learn, ya gain.”
“You can do anything you want to do. This is your world.”

And I love that they love these words of wisdom. You can find more here.

For Christmas this year, my son and I received Bob Ross T-shirts. Connor’s has just an image, while mine has a quote as well:

Bob Ross was referring to painting when he said these words; “In painting there are no mistakes, just happy accidents.” In other words, when you paint your mountain the wrong shape, treat it as a happy accident. It can still be a mountain, there may just end up being a happy tree or a happy cloud that takes care of your happy accident.

I think it works for math class, too. Recently, I modeled a Desmos lesson for a 7th grade teacher. The students had been working with expressions and equations but were struggling with the abstract ideas associated with expressions and equations. The teacher and I planned for me to model Desmos using Central Park to see how students reacted to the platform (this was their first time using Desmos) and how I managed the class using the teacher dashboard.

During the lesson, there was a lot of productive struggle. Students were working in pairs and making ~~mistakes~~ happy accidents. They were happy accidents! Because students kept going back for more. At times there was some frustration involved and I stepped in to ask questions like:

What are you trying to figure out?
Where did the numbers you used in your expression come from?
What do each of the numbers you used represent?
Before you click the “try it” button, how confident are you that the cars will all park?

The last question was incredibly informative. Many students who answered this question were not confident at all that their cars would all park, but as they moved through the lesson, their confidence grew.

One of the best take-aways the teacher mentioned during our post-conference was when she mentioned a certain boy and girl who she paired together so the (high performing) girl could help the (low performing) boy. The exact opposite happened. The girl was trying to crunch numbers on screen 5 with little success. The boy just needed a nudge to think about the image and to go back to some previous screens to settle some ideas in his mind before moving ahead with his idea that the answer is 8. Then, he got to expain how he knew it was 8 with the picture, conceptually, to his partner. The teacher’s ~~mistake~~ happy accident was in believing her students would always perform a certain way. When students are engaged in tasks that are meaningful, they tend to perform differently than when they’re given a worksheet with 30 meaningless problems on it (the norm for this class before Desmos). Ah-has all around and the “low student” shows that he knows more than the teacher thinks.

The icing on the cake? Several students walking out of the classroom could be heard saying, “That was cool.” or “That was fun.”

Let’s treat math mistakes as happy accidents, something to learn from and problem solve our way through. When students (all humans) make a mistake, synapses fire. The brain grows (More on this from Jo Boaler here). What we do as teachers from this point, determines how much more the brain will grow. If we treat student mistakes as happy accidents, perhaps their brains will grow a bit more than if we continue to treat mistakes in the traditional manner.

Let’s hear it for Bob Ross. He probably never thought his words of wisdom about painting would be translated to the math classroom.

Now, go make friends with a math problem.

The Best Part about Blogging

This is super exciting! I love it when teachers keep thinking – especially when I stop! What you’re about to read is truly the best part of blogging!

Readers of Under the Dome have been terrific commenters and questioners of my posts over the last 2 years and you all just keep getting better. Recently, Sharon Wagner, a teacher I met during a three-day summer institute in June visited my blog and reached out to share her ideas about the Olympic Cola Display 3-act task.

Sharon’s words:

Through the course of a few emails over the summer and a lot of my time spent doing things outside of the MTBoS (my lovely wife got some of her honey-do’s completed and I got some of my Mike-do’s finished) I have Sharon’s extension and am now posting it with her blessing! Please take a look. Her idea is a natural extension and allows students to design their own display using the colors of Coca-Cola twelve packs (which she most helpfully added to her document). Any Pepsi fans out there?

Sharon’s idea also ups the rigor by providing an audience (the merchant). This, again, is a part of that natural extension (of course someone designs these displays for the merchants). As for the Standards for Mathematical Practice . . . let’s just say your students will be engaging in multiple SMPs.

Again, this is super exciting. I love to share my ideas here, but when someone else takes it and makes it better – in this case by adding to it – everyone wins. Especially the students in our classrooms.

Thank you Sharon.

Sharon’s Display Extension:

coca cola display project extension

Math: A Fun After Homework Activity

All week long I’ve been asking Connor, my 9th grade son, what he has been working on in coordinate algebra. Here’s a snippet of a recent conversation:

Me: So, Connor, what have you been working on in your coordinate algebra class?
Connor: We’ve been graphing.
Me: Graphing what?
Connor: Graphing different lines.
Me: What kinds of lines are you graphing?
Connor: Ummmm…
Me: Are they linear functions.
Connor: Yeah, there are linear functions, but we also do curves…
Me: Like what kind of curves?
Connor: Umm… exponents
Me: Ok. Anything else?
Connor: Umm…
Me: Hey, I want to show you something. . .

Versions of this conversation happened several times this week. Due to soccer practices, games, homework, and Life in general, we never got much past Connor’s last “Umm…”

Until yesterday! The conversation changed a bit:

Connor: We did something cool in class today.
Me: Oh, yeah? What was it?
Connor: We had to build a picture using graphs of different lines. We built a shamrock.
Me: That’s what I’ve been meaning to show you all week. Go grab my laptop.
Connor: (playing game of war on an ipad) But I finished my homework.
Me: Just take a look at this for a few minutes and see what you think.
Connor: (heavy sigh)

Enter Des-Man from Desmos. Once he had gone through the tutorial, he was hooked. . . for a while! He engaged in this for about 2 1/2 hours. When he wanted to make something happen, but didn’t know how, he would come to me and ask. We’d figure it out together. The best part of this whole experience was when he realized he knew how to create something on his own and went to his math work from class as a reference.

Fast forward to 2 1/2 hours later, when Connor finished his Desman.

To see the picture in detail along with the equations Connor used to create this graph, click Connor Face Graph.

It didn’t stop there. I had some tabs open and clicked on one with the In-N-Out Burger task from Robert Kaplinsky. He was curious enough to work through it even after all of the Des-man work. So, I showed him more by clicking on the Open Middle tab (also from Robert Kaplinsky). I selfishly pulled up the task that I wrote in collaboration with Graham Fletcher called The Greatest Difference of Two Rounded Numbers. After making sense of the problem, and a lot of eye opening moments that led to phrases like “Oh, I can make it larger!” He got what he thought was the final answer and we validated his reasoning by clicking on the answer. A slight smile!

So, we’re looking at close to 3 hours of after homework math investigation that ranged from rounding numbers to graphing equations, and solving problems. Sounds like a great evening to me. Great conversations and fun while learning and reinforcing mathematics understanding! What could be better? Talking Math With Your Kids – High School Edition.

Feed the hunger of all ages!

More with Connor: Real Math Homework and Real Learning

Connecting Percents and Fractions

Not understanding mathematics can be extremely frustrating for students. As a teacher, figuring out how to help students understand mathematics can be just as frustrating. My primary go-to resource for these situations is Teaching Student-Centered Mathematics, by John Van de Walle et. al. because it’s all about focusing on big ideas and helping students make sense of the math they’re learning in a conceptual way.

Recently, I was asked to model a lesson for a 6th grade class who was having difficulty working with percents. So, I turned to my go-to resource, and during planning, I realized that I didn’t know anything about these students other than that they were struggling with percents. So, I couldn’t assume anything. I ended up creating three separate lessons and combined them into 1.

First, I handed groups of students a set of Percent Cards and Circle Graph Cards. Their task was to match the percent with the corresponding circle graph. As students were working on this, I heard groups reasoning about how they were matching the cards. Many started with benchmarks of 25%, 50%, and 75%, while others started with the smallest (10%) and matching it to the graph with the smallest wedge. As groups finished, they were asked to find pairs, using the matches they made, that totaled 100%. Once finished, a discussion about their process for completing these tasks revealed a solid understanding of percent as representing a part of a whole.

Now to shake their world up a bit. I asked them to leave their cards because they would be using them again shortly. I introduced these Percent circles and asked them what they were. A brief discussion revealed some misconceptions. Some students said they were fractions, others said they were wholes because nothing was shaded. I altered my planned line of questioning to questions that eventually led to a common understanding of what fractions were and how the pictures of the fraction (percent) circles really showed wholes and parts (fractions).

Their next task was to match their cards with the equivalent fraction circle. This was incredibly eye-opening. Groups began to notice that some percent card matches could fit with multiple fraction circles (50% could be matched with the halves, quarters, eighths, and tenths). Thirds and eighths were the last to be matched. But their reasoning didn’t disappoint. One group noticed that the percents ending in .5 all belonged with the eighths because they were too small to be thirds (the other percents with decimals).

Students were eager to share their thoughts about what they learned about fraction circles and percents:

Fractions and percents are the same because the pieces look the same.
1/4 is the same as 25% and 2/8
I don’t get why the eighths end in .5.
The percents all can be fractions.
1/8 is 12.5% because it’s half of 25%

Finally, I asked students to solve a percent problem (now that they’ve all realized that fractions and percents can be used interchangeably). I gave them the m & m problem from this set of percent problem cards. The only direction I gave was that they had to solve the problem using some representation of the percent in the problem before they wrote any numbers.

My bag of M&M’s had 30 candies inside. 40% of the candies were brown. How many brown candies is that?

While this was problematic at first, students looked at their fraction circles and percent cards and realized they could use four of the tenths since each tenth was the same as 10%. Most students needed just one “least helpful” question to get on the right track: Where do the 30 m & m’s belong in your representation?

Most groups were able to make sense and persevere to solve the problem correctly, and explain why they “shared the 30 m & m’s equally among the ten tenths in the fraction circle” and why they “only looked at four of the tenths because that’s the same as 40%.”

My beliefs that were reinforced with this lesson:

We can’t assume understanding from correct answers alone. We need to listen to students reason through problematic situations.
Students really want to share their thinking when they realize that someone is really interested in hearing it.
Students crave understanding. They really want to make sense.
Procedures are important, but not at the expense of understanding.
Empowering students by allowing them to build their own understanding and allowing them to make connections allows students to feel comfortable taking risks in problem solving.

Please take a look at Jenise Sexton’s recent blog about percents with 7th grade students for some fantastic ideas about students using number lines and double number lines to solve percent problems. It’s SWEET!

Empowering Students with In-N-Out Burger

The following is a reflection on a 3-Act task I modeled for an 8th grade teacher last week. The 3-Act is In-N-Out Burger from Robert Kaplinsky and the plan I followed I completely stole from the amazing @approx_normal ‘s blog post on her work with the same 3-Act with administrators last year.

This past Thursday was the day we agreed on to model the lesson. So, this group of 8th grade students, who have never even seen me before, are wondering who this guy is that’s about to teach their class. And, just as planned, they were giving me weird looks when I showed them the first cheeseburger picture and asked them what they noticed. I believe one of them even asked, “Are you a teacher?”

Fast forward through to the “What do you wonder?” piece and the questions were amazingly well thought:

“How much weight would you gain if you at that whole thing (100×100 burger?)”
“How much do the ingredients cost for it (100×100 burger)?”
How much does it (100×100 burger) cost?
“Why would someone order that (100×100 burger)?”
“Did someone really order that (100×100 burger)?”
“How long did it take to make the (100×100 burger?)”

There were just a couple more, and they all came up very quickly. The students were curious from the moment we started the lesson. They are still working on precision of language. The parentheses in their questions above denote that this phrase was not used in the question, but was implied by the students. We had to ask what “it” or “that” was periodically throughout the lesson as they worked and as time went on, they did become more consistent.

The focus question chosen was:

How much does it (the 100×100 burger) cost?

Students made estimates that ranged from $20 to $150. We discussed this briefly and decided that the cost of the 100 x 100 burger would be somewhere between $20 and $150, and many said it would be closer to $150 because “Cheeseburgers cost like $1.00, and double cheeseburgers cost like $1.50, so it’s got to be close to $150.” That’s some pretty sound reasoning for an estimate by a “low” student.

As students began Act 2, they struggled a bit. They weren’t used to seeking out information needed, but they persevered and decided that they needed to know how much a regular In-N-Out cheeseburger would cost, so I showed them the menu and they got to work.

I sat down with one group consisting of 2 boys (who were tossing ideas back and forth) and 1 girl (Angel) who was staring at the menu projected at the front of the room. She wasn’t lost. She had that look that says “I think I’ve got something.” So, I opened the door for her and asked her to share whatever idea she had that was in her head. She said, “Well, I think we need to find out how much just one beef patty and one slice of cheese costs, because when we buy a double double we aren’t paying for all of that other stuff, like lettuce and tomato and everything.” The boys chimed in: “Yeah.” I asked them how they would figure it out. Angel: “I think we could subtract the double-double and the regular cheeseburger. The boys, chimed in again: “Yeah, because all you get extra for the double double is 1 cheese and 1 beef.” “Well done, Angel!” You helped yourself and your group make sense of the problem and you helped create a strategy to solve this problem! Angel: (Proud Smile)!

We had to stop, since class time was over. Other groups were also just making sense of the idea that they couldn’t just multiply the cost of a cheeseburger by 100, since they didn’t think they should have to pay for all of the lettuce, tomato, onion, etc.

They came back on Friday ready to go. They picked up their white boards and markers and after a quick review of the previous day’s events and ah-ha moments, they got to work. Here is a sample after about 15 minutes:

Many groups had a similar answer, but followed different solution pathways. I wanted them to share, but I also wanted them to see the value in looking at other students’ work to learn from it. So I showed this group’s work (below-it didn’t have the post-its on it then. That’s next.). I asked them to discuss what they like about the group’s work and what might make it clearer to understand for anyone who just walked in the classroom.

Shared Student Work

Here’s what they said:

I like how they have everything one way (top to bottom).
I like how they have some labels.
I’m not sure where the 99 came from. Maybe they could label that.
Where’s the answer…

During this discussion, many groups did just what @approx_normal saw her administrators do when she did this lesson with them. They began to make the improvements they were suggesting for the work at the front of the room. It was beautiful. Students began to recognize that they could make their work better. After about 5 minutes, I asked the class to please take some post-its on the table and do a gallery walk to take a close look at other groups’ work. They were to look at the work and give the groups feedback on their final drafts of the work using these sentence starters (again, from @approx_normal – I’m a relentless thief!):

I like how you. . .
It would help me if you. . .
Can you explain how you. . .

Some of the feedback (because the picture clarity doesn’t show the student feedback well):

I like how you showed your work and labeled everything.
I like how you broke it down into broke it down into separate parts.
It would help me if you spaced it out better.
I like how you explained your answer.
It would help me if it was neater.
I like how you explain your prices.
I like how you wrote your plan.
I like how you explain your plan.
I like how you told what you were going to do.
Can you explain how you got your numbers.
I like how you wrote it in different colors.
It would help me if you wrote a little larger.

Some samples with student feedback:

Not only was the feedback helpful to groups as they returned to their seats, it was positive. Students were excited to see what their peers wrote about their work.

Now for the best part! Remember Angel? As she was packing up to leave, I asked her if her brain hurt. She said, “No.” After a short pause she added, “I actually feel smart!” As she turned the corner to head to class, there was a faint, proud smile on her face. Score one for meaningful math lessons that empower students.

Please check out the websites I mentioned in this post. These are smart people sharing smart teaching practices that are best for students. We can all learn from them.

Math Students are Bleeding Out!

Let me explain. There’s a math epidemic (remember Ebola 2014+). Students are bleeding out from the gashes of their misconceptions of mathematics. The lack of teaching conceptual understanding along with sacrificed opportunities to make mathematical connections is the double edged sword. This is an epidemic, and some teachers, school systems and educational leaders are treating it like it’s a tiny scratch, instead of the pervasive threat to mathematical achievement that it is.

Here’s a familiar scenario: A school’s test scores come back after the spring testing season (or mid-terms). The scores show little growth from the previous year in the area of mathematics, and any change is not in a positive direction. The knee-jerk reaction to the valid question, “What can we do to fix this?” is to look for programs and technology that will fix the problem. These are the same individuals who, way back in August, looked us all in the eye and, with the greatest of sincerity, reminded us that the single most important factor determining student success is the quality of the teacher. Not new programs. Instead of growing the quality of teachers, we get programs that:

push speed over comprehension (imagine if we taught reading this way).
define fluency based on digits rather than efficiency, flexibility, and accuracy.
use technology to separate us from our students when we know that what we really need is to spend more time listening to them and creating an interactive classroom with technology as a support for this human interaction
are essentially Band-Aids

I often hear the phrase “back to the basics” in times like these. I’ve heard parents, administrators, and even a few teachers say this. I think everyone would agree that “back to the basics” should mean that students become computationally fluent. The idea of going back to this implies that we were doing something right before. And we all know that’s not true. After all we have generations of adults who are not computationally fluent and/or have extreme math anxiety. And how did that happen?

Answer 1: Timed tests. My sixth grade teacher called them speed tests. We did them every day, right after lunch. (I was never in the top 10).

Answer 2: Algorithms memorized by students with no understanding, presented by teachers with little understanding other than from a teachers’ edition.

Answer 3: Little or no real problem solving. Naked computation all around. No wonder students were turned off by mathematics!

Answer 4: No interaction. Math is a social activity. If you talk to any engineer, designer, architect, mathematician, statistician, etc. They aren’t doing their work in an office silently sitting in rows. They’re constantly talking to one another about the mathematics they’re using. The idea that all of us are smarter than one of us makes so much sense in the real world and it should make sense in the classroom as well.

If we went back to teaching math like we did 20-30 years ago (I think that’s what some of these folks were implying when they said “back to the basics.” We’d still be in the same boat. Anyone ever watch How old is the shepherd?. That was popularized over 20 years ago and the results haven’t changed. Going back is not an option. Building fluency is.

So what do we need to do in math classrooms? I have a few ideas to stop the bleeding and these are certainly not original to me.

Apply pressure to the wound. Give up on the ineffective treatment, not the patient. Apply pressure to stop the bleeding. Focus on tasks and activities that build number sense. Number Talks, Math Talks, Estimation 180, Visual Patterns any or all of these can be put in place at any level. And the best part is, students can easily be trained to begin to apply the pressure themselves. They have the power to stop the bleeding!
Close the wound. This can only happen with stitches. And it takes time to get the hang of it. The wound has to be closed with the thread of understanding. We can’t understand for them, so the wound has to be closed with the help of the students. The students create this thread as we stitch and we can’t do it without them. How do they create this thread of understanding? We have to stop telling so much and instead “be less helpful.” If we tell students too much, the thread breaks.
Treat any symptoms that may show up after the initial treatments above:

Symptoms	Name	Treatment
Students may begin to rely on rote procedures with no foundational understanding Sometimes unintentionally caused by parents & other adults trying to help.	Misconceptionitis	Identify the misconception(s) and re-build understandings using the CRA (Concrete Representational Abstract) model
Students are finding unreasonable solutions to tasks & problems and they often seem unaware; clueless	Unreasonableness	This is often attributed to students just not thinking enough. Treatment should include a DAILY diet rich in estimation – prescribe www.estimation180.com
Students count (often on fingers when computing or rely on a calculator for the simplest of calculations and even then, they can get incorrect answers.	Influencia	This is often diagnosed along with unreasonableness (see above). Its roots lie in naked computation and memorization of facts rather than allowing students to build strategies and practice those strategies until they become fluent. First, counting strategies are the lowest level strategies. Students need to build more efficient strategies by exercising with investigations of number relationships through number talks, math talks, and strategy building. Stop giving speed tests.
Students have strategies for computation, but are not applying them in problem solving situations	No Solvia	Students need a heavy dose of problem solving every day. This must involve students engaging in the Big 8 Standards for Mathematical Practice. Problem solving tasks every day. Hydrate often with student reasoning. Adopt the classroom mantra: “The answer isn’t good enough.” Begin new concepts with a problem before any formal instruction on the topic. See what students can do before assuming what they can’t do.

I’m a teacher and I know many of you reading this are the choir that need no preaching to. If you’re interested in saving the patient, stopping the bleeding, and raising math achievement, click on some of the links in this post. There’s so much to learn from those smarter than me. Also check out #MTBoS on Twitter. Lots of math goodness from the best out there.

Click here and here to learn more about strategy development. Great stuff from www.nzmaths.co.nz!

The Penny Cube

I just finished a 5th grade 3-Act task called Penny Cube that I created last spring. I tried it then, but just to get some feedback from students and see what I might need to change about how the task should be presented. Now, after completing this task with two groups of students (at two different points in the year), I’ve learned three things:

Students see a video and notice a bunch of things that teachers don’t even realize are there.
The curious questions students ask first are often “why” questions.
There’s no way to predict everything a group of students might wonder.

I’ll take this reflection from the beginning. First, I let students know that I was going to show them a video clip. I also told them that I was going to ask them what they noticed when it was finished playing. I gave students a chance to brainstorm ideas about what they could do to make sure they would be able to share what they noticed once the clip had finished playing. Their ideas were amazing:

We could look for expressions (on faces – I found out later that this student was thinking about context. A person’s facial expression can tell a lot) Unfortunately, there were no facial expressions in this video.
Listen carefully (they might be able to hear something that might give them a clue about what was going on – these students were already expecting a problem situation!)
Stay focused on the clip.
Take notes.
Try to remember as much as you can.

I had never done this before, but after hearing their ideas, I will be using this again.

After showing the video clip for Act 1, I immediately had them talk about what they noticed with their groups. Then, they were asked to share with the whole group. Here is what they noticed:

What’s missing from this picture is the wonderful reasoning given for some of these. For the last bullet, “container is open in the front,” the student told the class that it was open in front so the pennies could be placed in the container more easily (I never thought they’d see or think about that). They even began to wonder a bit here – “it might be an expression or it might be counting.” My favorite, though, is the estimation by the girl who said “it looks like 100 pennies in the stack ($1.00).” This was particularly interesting to me because of what happened when they were asked to estimate for the focus question.

The wonders were typical from what I usually get from students new to 3-Act tasks, but I handled it a bit differently this time. Here are their wonders (click here for a typed version of Penny Cube Notices&Wonders):

In my limited (yet growing) experience with teaching using 3-Act tasks, I’ve noticed that the wonders are initially “why” questions (as stated in number 2 above). I told the class that I noticed that the questions they were asking were mostly “why” questions. I asked them what other words could be used to begin questions. Rather than trying to steer students to a particular question, I decided to focus the students’ attention on the kinds of questions they were already asking, and guide them to other types of questions. It didn’t take long! Within about 5 minutes, students had gone from “why” questions to “how many . . .” and “how much . . .” questions which are much easier to answer mathematically.

The students were then asked to figure out what they needed to solve the problem. From experience with this task, I knew that most students would want pennies, so I had some ready. I didn’t give them the Coin Specifications sheet, because no one asked for it. I did have it ready, just in case. Every group asked for pennies and rulers. I wasn’t sure how they would use them, but I was pleasantly surprised.

Here’s what they did:

How many pennies in 2 inches

How many pennies in an inch

How many pennies fit on a 6 inch edge of the base

How many pennies cover base

How many stacked pennies in 2 inches?

The students all started in a place that made sense to them. Some wanted to figure out how many in the stack, so they stacked pennies and quickly realized (as I did when filling the cube) that you can’t stack pennies very high before they start to wobble and fall. So, they measured smaller stacks and used that info to solve the problem. Others wanted to find number of pennies along an edge to find how many cover the base, then work on the stacks. Students were thoroughly engaged.

After three 1 hour classes, students were wrapping up their solutions. Some groups were still grappling with the number of pennies in a stack. Others were finished. A few were unsure about what to do with some of the numbers they generated. All of this told the classroom teacher and me that there were some misconceptions out there that needed to be addressed. Many of the misconceptions had to do with students disengaging from the context, rather than integrating their numbers into the context:

One group was unsure of whether to multiply the number of pennies in a stack by 12 (6 inches + 6 inches) or to use 64.
Another group found the number of pennies to cover the base and multiplied it by itself to get their solution.
A third group found 37 pennies in 2 1/2 inches and was having a difficult time handling that information.
A fourth group had come up with two different solutions and both thought they were correct. Only one could defend her solution.

Eventually, several groups arrived a solution that made sense to them.

Time to share!

I chose one group to share. This group had a reasonable solution, but their method and numbers were different from many of the other groups, so this is where we were hoping for some light bulbs to begin to glow a bit.

This group shared their work:

I asked the class what they liked about the work. The responses:

The math (computations) are written neatly and they’re easy to follow.
I know what their answer is because it has a bubble around it.
The question is on it.
It’s colorful.

All good. Now, for the best part:

What questions do you have for this group? The responses:

Where did you get 34?
What does the 102 mean?
How about the 64?

Any suggestions for this group to help them clarify their work to answer some of your questions?

Maybe they could label their numbers so we know what the numbers mean.
Maybe they could tell what the answer means too. Like put it in a sentence so it says something like “6,528 pennies will fit in the container.”
Maybe they could have a diagram to show how they got a number like 64 or 34. I know that would help me (this student had a diagram on his work and thought it was useful).

The light bulbs really started to glow as students began making suggestions. As soon as a suggestion was made, students began to check their own work to see if it was on their work. If it wasn’t, they added it. All of the suggestions were written on the board so they could modify their work one final time. The best part about this whole exchange was that students were suggesting to their peers to be more precise in their mathematics (SMP 6 – Attend to precision). And, they really wanted to know what 34 was because they didn’t have that number on their boards (which is why I chose this group).

Now for the reveal! When I asked the class if they wanted to know how many pennies were in the cube, they were surprised when I pulled up the reveal the video. I guess they thought I’d just tell them (that’s so 1980’s). They watched to see how close they were and when the total came up on the screen, many cheered because they were so close!

The students in this class were engaged in multiple content standards over the course of 3 days. They reasoned, critiqued, made sense, and persevered. It’s almost difficult to believe that this class was a “remedial” class!

Below, I’ve included a picture of each group’s final work.

Finally, one of the conversations witnessed in a group was between a girl and a boy and should have been caught on video, but wasn’t. This group had an incorrect solution, but they were convinced they were correct, so to keep them thinking about the problem, I asked them how many dollars would be equal to the number of pennies in their answer (3,616).

Girl: There are 100 pennies in a dollar. So 600 pennies is . . .
Boy in group: $6.00
Girl (after a long pause): 1,000 pennies equals $10.00
Boy: So that’s . . . um. . .
Me: How does knowing 1,000 pennies = $10.00 help you.
Girl: We have 3,000 pennies, so that’s $30.00.
Boy: $36.00
Me: Share with your group how you know it’s $36.00
Boy: Because $30.00 and $6.00 is $36.00
Girl: And the rest (16) are cents. $36.16!

And they didn’t even need a calculator!

Math really does make sense!

So…Have You Always Taught Math This Way?

I’ve been asked this question several times over the past 15 years or so. Most recently at a workshop I facilitated for middle school teachers. The short answer is no. My teaching has evolved. I strive to improve my practice every day. Below, is my response to the group of middle school teachers.

When I first started teaching, I used what I learned in college about teaching mathematics – you know . . . using manipulatives, group work, classroom discussions. All of those things that I still use today. But, when things didn’t go the way I anticipated, I seemed to always fall back on the way I learned which was primarily stand and deliver.

At the end of my first year, I spent some time in my room, at my desk and wrote down all of the changes I wanted to make and how I planned to make them. This was probably the best idea I ever had! Throughout the summer I reread that list and, when necessary, created things that would help me reach my goals. I didn’t reach them all, but the next year was much more successful. Couple that with the summer PL that I took and the way I was teaching math was really beginning to change.

One of the first changes I made was to incorporate children’s literature into my lessons. One of the PL’s I took that summer was a Marilyn Burns workshop where we learned that there are a tremendous number of books with mathematical connections. We learned how use the books to introduce mathematical concepts and problem solving, how to ask better questions, and one of my big “take-aways” was to listen more!

Over the years, I’ve continued to look at literature as a place to begin lessons. And all was going well, but I still wasn’t getting the the amount of buy-in from my students that I wanted. I was excited about the math, but they weren’t. Then, one morning, I was riding to work with my wife, Kim. We were listening to a morning radio show in Atlanta on 99x called the Morning X with Barnes, Leslie, and Jimmy. On that morning, November 10, 1999, Jimmy was laughing about a news story that he couldn’t wait to share. As he was reading, I was scrambling to write it all down! The story went like this:

Earlier this morning a man held up a GA-400 toll booth. His stolen getaway car broke down and he is now on the run with a 58 lb. bag of quarters.

When I got to school, I turned on my computer, printed the story out on a transparency with a picture of some quarters and put it on the overhead. Here’s a sample of what happened:

GA400_Screenshot

Several students as they entered the classroom: Mr. W., what’s that on the overhead?

Me: I heard that on the radio this morning and wanted to know what you all thought and if you had any questions.

Multiple student responses: “Oh, ok.” “That guy is stupid.” “What kinds of questions do you want?

Me: Whatever questions come to mind. You can write your thoughts and questions in your journal.

What I got from these 5th grade students at the beginning of class amazed me. They were totally engaged in the problem. The problem context had them so curious, they wouldn’t let go.

Some of their questions:

How many quarters is that?
How much money is that?
How tall would a stack of 58 lbs of quarters be?
How far could you run with a 58 lb bag of quarters?
How big is the bag of 58 lbs of quarters?
How long would a trail of 58 lbs of quarters be if they were laid end to end?

This one context from a morning radio show kept my students focused on the mathematical concepts of weight, length, decimal computation, and time for over a week. More questions came up as new ones were answered. They had developed not only a curiosity, but an intellectual need to know.

This is what I had been searching for. A context that engaged my students in mathematics so deeply, that they wanted to figure out the answers to their own questions.

It wasn’t easy to find stories like this back then. But now, they’re everywhere. Just Google bizarre news stories. Since then I’ve learned, along with a whole host of others (check out some of the people I follow), that I can create these contexts using all sorts of media to get the same results (3-Act Tasks).

Below is a copy of the original context I used with my students. The image has changed over the years, but it is essentially the same document. And it works just as well today as it did 15 years ago! I just wish I had a recording of the news story! If you decide to use this, please share your experience. I’d love to hear about it!

GA400 toll problem

	mwiernicki on Relevant Decimals Lesson
	Ella on Relevant Decimals Lesson
	Dividing Decimals an… on Relevant Decimals Lesson
	mwiernicki on Real Math Homework and Real…
	Norah A on Real Math Homework and Real…

Teaching the Game

Hubbub Materials

Share this:

Day 1

Day 2

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this: