Georgia’s new state school superintendent, Richard Woods, recently wrote a column about teaching mathematics. “Funny math methods” was the catch-phrase taken from the article and sent out through the media. This was not unexpected. Frankly, I’m surprised it took this long. This was part of his campaign platform.
Though his column has prompted some emotional responses from math educators, it is imperative that this significant dialogue he has opened, continue. The best thing we can do for the students of Georgia is to keep this discussion going in order to come to a common understanding about the mathematical terms, strategies and ideas presented by Mr. Woods in his column. We can truly help the students of Georgia by making sure we are all speaking the same language.
Since I am unable to respond directly to Mr. Woods’ column, I would like to continue the dialogue here. I welcome any and all comments that keep this discussion moving forward in a positive light. I encourage all viewpoints, since one-sided dialogues don’t tend to be very productive.
Mr. Woods talks about hearing from parents unable to help their children with their math homework. I, too, have heard this from parents. My response to this is: If students are not able to do their homework independently, perhaps it should not have been assigned. This is difficult for many to hear. If you think about it, though, it really makes sense. If we want students to build their understanding of mathematics based on what they have learned, we have to make sure they have learned it before they can build on it. That said, I look at homework as falling into one of three categories:
- Practice – students use understandings learned in class to practice and build a more solid understanding at home.
- Preview – students are given a few problems to get them thinking about a new concept that is related to what they already know.
- Extension – students take a problem or task they worked on in class and are asked to extend their understanding. For example, in middle school, students may discover a growth pattern and as an extension, they may be asked to create a growth pattern that grows twice as fast.
Notice that each of these types requires students to have an understanding before they begin. Understanding in mathematics, as in reading, is crucial for student success.
Mr. Woods also mentions the need for students to have a firm understanding of the fundamentals of mathematics. He goes on to say that basic algorithms, fact fluency, and standard processes for addition, subtraction, multiplication, and division contribute to building that strong foundation for student achievement.
This is interesting. First, algorithms have gotten a bad rap. But, there is a place for algorithms in the big picture of how students learn mathematics. An algorithm is just a mathematical term for a series of steps that can be followed to determine a solution to a mathematical computation. Problems occur when algorithms are taught just as a series of steps to memorize, rather than facilitating an understanding of the computation(s) first. Without understanding, the steps often don’t make sense and one or more of three things may happen next:
- Students may complete algorithmic steps out of order.
- Students may skip one or more steps of the attempted algorithm.
- Students may confuse the steps of one algorithm with another.
These may seem like easy fixes -“just tell the students again”. Telling them where their errors are and having them practice more problems does not work. Without a conceptual understanding of what the computation means, students will continue to make these errors. Though students may be able to show some success in the short term, over the long term they will revert back to one or a combination of the error patterns above.
Completing algorithms incorrectly doesn’t even compare to one of the worst side effects of this procedural teaching: students who don’t realize their answers are unreasonable. For example, a teacher recently sent me the email below:
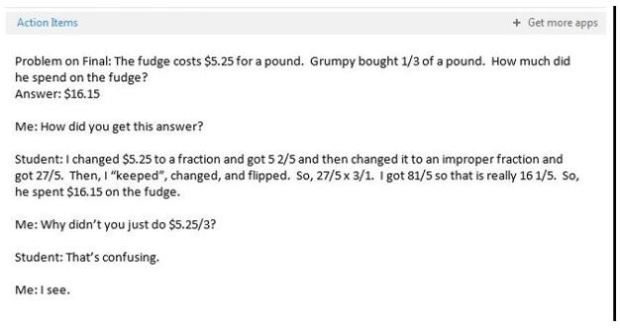
This student has some major misconceptions. With a conceptual understanding, this student could have reasoned that 1/3 of a pound is less than a whole pound, so the answer should be less than $5.25. Without conceptual understanding, the student is attempting to recall and use procedures they do not understand, is confusing procedures, and is unable to determine whether or not the solution they have found is reasonable. This is only one piece of numeracy that is lost in the procedural mathematics instruction that Mr. Woods seeks.
Fact fluency and the standard procedures for the four basic operations is next. I don’t think there is a math teacher anywhere in the world that doesn’t think fluency is important. In order to be clear though, memorization and fluency are not the same thing. Not even close. To keep this short and sweet, with the focus on students, I have copied the excerpt below from the GA DOE frameworks for mathematics. I think this sums everything up nicely (no pun intended). However, if you would like to learn more about fluency, click the links below.
Fluent students:
- flexibly use a combination of deep understanding, number sense, and memorization.
- are fluent in the necessary baseline functions in mathematics so that they are able to spend their thinking and processing time unpacking problems and making meaning from them.
- are able to articulate their reasoning.
- find solutions through a number of different paths.
For more about fluency, see: http://www.youcubed.org/wp-content/uploads/2015/03/FluencyWithoutFear-2015.pdf and: http://joboaler.com/timed-tests-and-the-development-of-math-anxiety/
The fundamentals that Mr. Woods should have mentioned are actually reasoning and sense making. This is what it takes to learn and do mathematics. So, again, understanding must take place. However, understanding cannot take place through the memorization of algorithmic steps alone. This is not just what I think. It’s what I know from years of teaching students mathematics. This is also backed by research, papers, & videos. The building of understanding is also fostered through a passionate, grassroots movement of mathematics teachers #MTBoS (Math Twitter Blog-o-Sphere). This is our place to collaborate, share, and work to improve our teaching of mathematics.
Next, Mr. Woods discusses teaching “funny math methods.” He specifically mentions “the lattice method” and he correctly states that this method is not state mandated and not required for students to achieve on state tests. Mr. Woods is absolutely right! This is not state mandated because it is a ridiculous strategy for multiplying multi-digit whole numbers. to be fair, it works – every time. If you follow the steps of this algorithm by making the grid correctly, and placing the digits of the numbers correctly in the grid, and placing the products of the digits in the right places, and drawing the diagonals correctly, and adding the digits along the diagonals correctly, and copying the product correctly from the grid written in standard form. You think that’s ridiculous? Here’s something even worse – it’s often used for those students who have trouble remembering the steps of the standard algorithm. This method is the definition of “funny math” and math teachers should not use this since it is does not make sense to students (or teachers) and it does not align with any of the standards for multiplication.
Mr. Woods says that mathematics has become over complicated. It hasn’t. It is only as complicated as it has been for centuries and that complication is exacerbated through teaching without sense making. We can teach students to think mathematically on their own. We can support and help them grow through their own understandings of mathematics. We can help students make sense of mathematics and learn to use this to make informed decisions, rather than listening to others make these decisions for them. We can do this because what we know now is how students learn mathematics. It is not through memorization. It is through sense making and reasoning. What we know now is that teaching students to think mathematically, through problem solving by building conceptual understanding provides students experience and allows them to make connections to algorithms they create and those created by others. What we know now is that this works best for all students. Not just average students, or above average students, or below average students. All students.
Finally, just to be clear:
- We (mathematics teachers) are most likely more current than most on research-based, best practices in the mathematics classroom.
- There is a place for the algorithms you wish to see in the classroom, and they are found in the appropriate grade level standards. However, using an algorithm is not the end-all, be-all for learning mathematics. There is always a need for students to be flexible, efficient, and accurate in their computations. Multiple strategies, based on student understanding, must be explored.
At the end of the column, Mr. Woods states that “Offering choices and clarification are some of the steps we are taking to address the concerns surrounding mathematics in our state.” I applaud these steps. Choices are always a good idea. Clarification is even better! Let’s work together to clarify the misconceptions about best practices in mathematics instruction. Armed with these common understandings, Georgia can lead the charge as a state united to raise student achievement in mathematics.
I look forward to all comments and continuing this dialogue to help build these common understandings.